(関連記事)
「相似」は算数の多くの問題で関連するのできちんと理解しましょう。
相似のテクニック
1)2組の角度が同じならその三角形どうしは相似になる
2)相似の三角形の辺は比例関係から求められる(事が多い)
3)直角三角形の中に正方形が入った問題は相似の三角形を作って解く
(算数における)相似とは?
相似(そうじ)とは、
●大きさが拡大や縮小の関係となっている図形●
●相似関係にある図形では、対応する角度と、対応する辺の比が同じになる●

この二つの三角形は相似で、相似比は2:3となります。
相似のテクニック

相似については、以下の点をテクニックとして覚えてください。
相似のテクニック
1)2組の角度が同じならその三角形どうしは相似になる
2)相似の三角形の辺は比例関係から求められる(事が多い)
3)直角三角形の中に正方形が入った問題は相似の三角形を作って解く
1)2組の角度が同じならその三角形どうしは相似になる

2組の角度が同じならその三角形どうしは相似になる
これは、必然的に残りの角度も同じになるので、全ての角度が同じ
三角形どうしとなりますよね?ですので必ず相似になります。
ポイントは、「2つの角度が同じだな→相似!」という発想というか
テクニックというか、まあその辺です。
これは説明いらないですよね?
2)相似の三角形の辺は比例関係から求められる(事が多い)

●相似関係にある図形では、対応する角度と、対応する辺の比が同じになる●
これも分かるかと思います。
問題)辺ADの長さは?
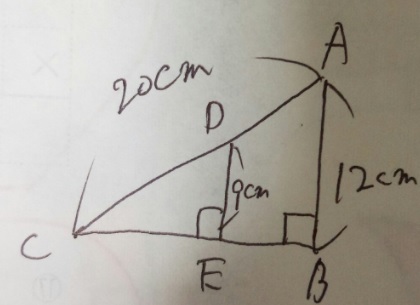
1)2つの角度が同じ→相似
2)相似比は9:12→3:4
3)AC20:CD=4:3=20:15
4)AD=5 答え)5cm
3)直角三角形の中に正方形が入った問題は相似の三角形を作って解く
直角三角形の中に正方形が入った問題は相似の三角形を作って解く
これは、問題と図を見るのがいいでしょう。
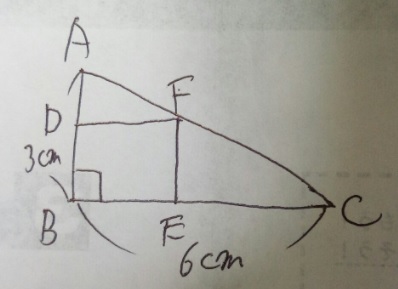
問題)DFBEは正方形です。1辺の長さは?

1)ABCとADFは相似(2つの角度が同じだから)
2)BC2:BA1なので、DF:DAも2:1
3)正方形なので全部の辺が同じ長さだから、DF=DB
という事は、DB:DAも2:1
4)AB3cm=DB(割合2)+DA(割合1)、割合1=1cm
5)DB=2cm
答え)2cm
直角三角形の中に正方形が入った問題は相似の三角形を作って解く
相似+三角形のテクニック3つ!の中学入試問題等
問題)浅野中学(問題文はワイが簡略化してます)
2つは同じ三角形です。DEFGは正方形です。正方形の1辺の長さは?
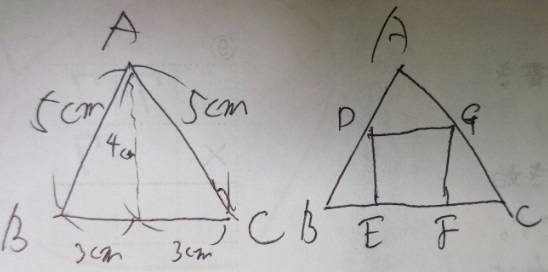
1)BCの中間(Aから直線を引く)をHとします
2)三角形AHBと三角形DEBは相似(2つの角度が同じ)。相似比はまだ不明
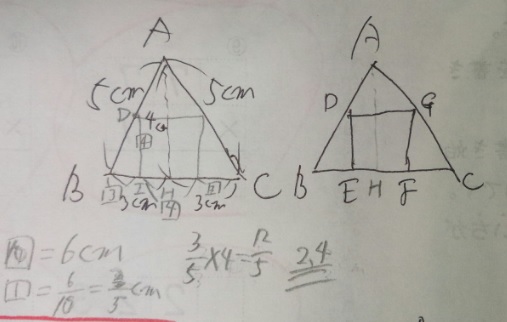
3)三角形AHBのAH4:HB3。相似なのでDE④:EB③の割合も同じとなる
4)(正方形なので)DE=EF。EFは割合④、FCは2)3)と同じ理屈で割合③
5)BC=6cmで、BE③+EF④+FC③。6cm=割合⑩
6)割合①=6÷10=3/5
7)正方形の1辺はEF、割合④なので3/5×4=12/5=2.4
答え)2.4cm

まとめ
「相似」は算数の多くの問題で関連するのできちんと理解しましょう。
相似(そうじ)とは、
●大きさが拡大や縮小の関係となっている図形●
●相似関係にある図形では、対応する角度と、対応する辺の比が同じになる●

相似のテクニック
1)2組の角度が同じならその三角形どうしは相似になる
2)相似の三角形の辺は比例関係から求められる(事が多い)
3)直角三角形の中に正方形が入った問題は相似の三角形を作って解く

(関連記事)