(関連記事)
この記事を読む前に必ず「相似+三角形のテクニック3つ!」を先に読んでください。
ポイントは「平行線+特定パターン→相似」を見抜く事です。
(パターンは「ピラミッド型」と「ちょうちょ型」です)
平行線と相似①:平行なら辺の比も同じになる
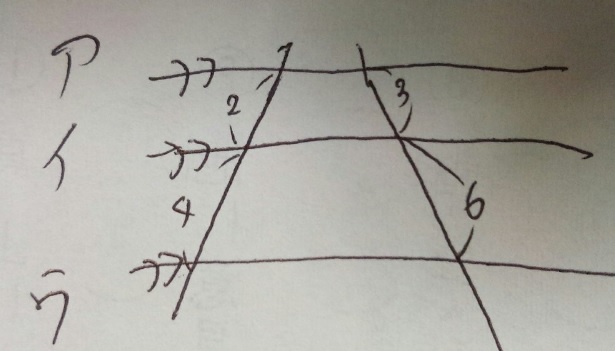
これは分かりやすいかと思います。平行である場合は、辺の比が移動できる
という事です。左の辺の比「1:2」が右の辺の比「1:2」と同じになります。
平行線と相似②:三角形(ピラミッド型)とチョウチョ型
「平行線と相似」の典型パターンは以下の二点です。
【三角形(ピラミッド型)の相似】
「三角形が重なる形(ピラミッド型)+平行→相似」という発想が大事です。
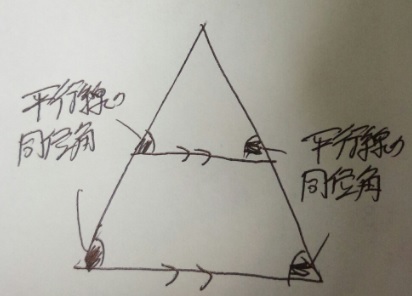
「二本の線が平行」→同位角が同じ→2角が同じなので相似の三角形
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
相似のテクニック
1)2組の角度が同じならその三角形どうしは相似になる
2)相似の三角形の辺は比例関係から求められる(事が多い)
3)直角三角形の中に正方形が入った問題は相似の三角形を作って解く
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
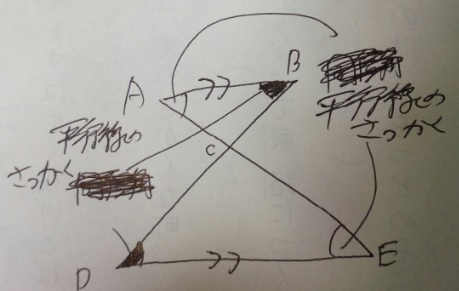
チョウチョ型の相似

三角形ACBと三角形ECDは相似(対応する角や辺を間違えないように!!)
理屈はピラミッド型と同じです。

「二本の線が平行」→錯覚が同じ→2角が同じなので相似の三角形
平行線+三角形の相似の中学入試問題等
問題)東邦大附属東邦中学
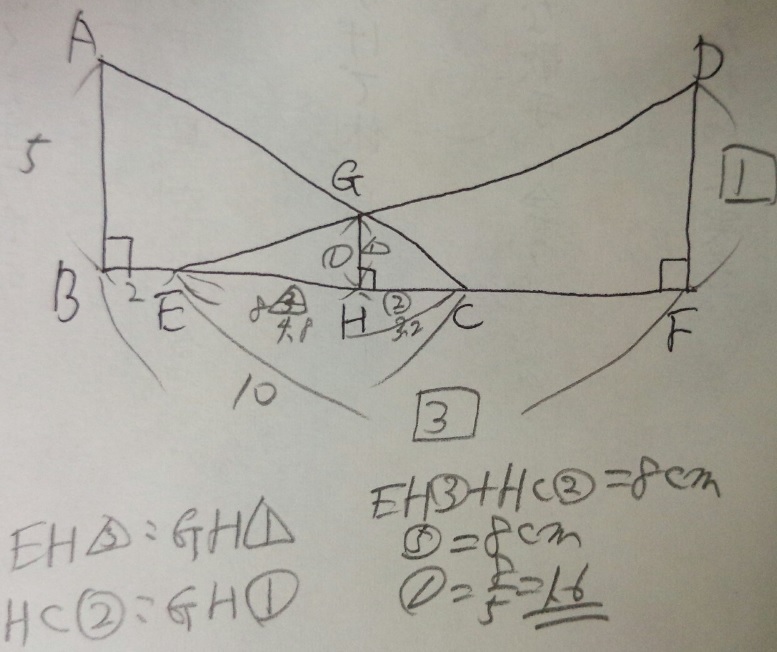
AB=5cm、BC=10cm、BE=2cm、EF:FD=3:1。GHは何cmですか?
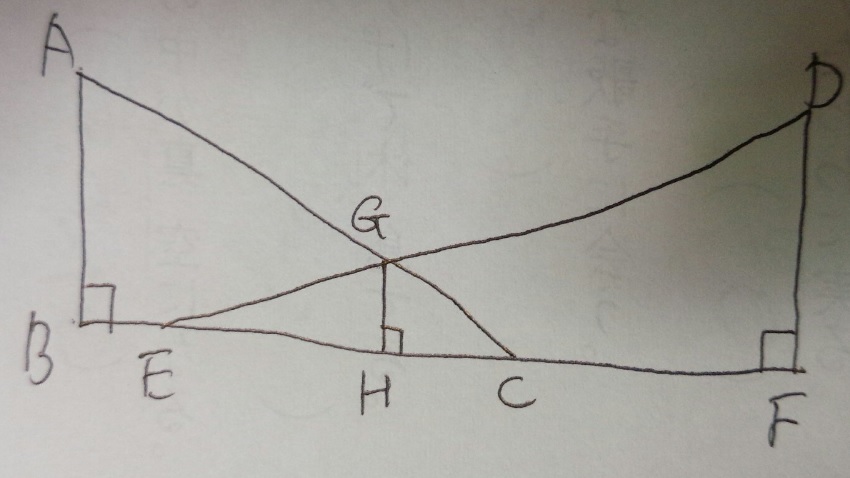
1)わかる数字を図に書き込みます(これを正確にやらずに問題解けません)
2)相似の三角形がたくさんありますね。
3)三角形EFDと三角形EHGが相似なので、EH:GH=「3」:「1」
4)(同じく)三角形CBAと三角形CHGが相似で、AB5cmBC10cm=①:②なので、
GH①:HC②
5)3)4)から、EH:GH=「3」:「1」かつGH①:HC②
GHが同じ割合1なのでEH割合3、HC割合2もそのまま使える
6)EH割合3+HC割合2=10cm-2cm=8cm。割合5=8cm、割合1=1.6cm
GHは割合1なので答え1.6cm
答え)1.6cm
問題)桐光学園中学
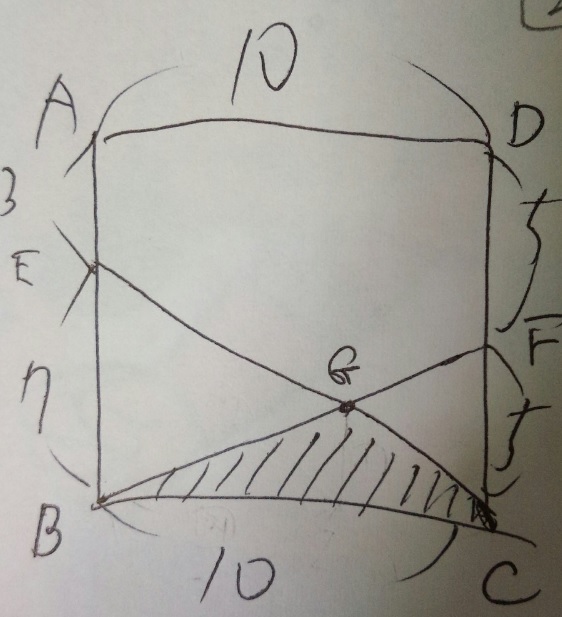
ABCDは正方形。斜線部分の面積□c㎡
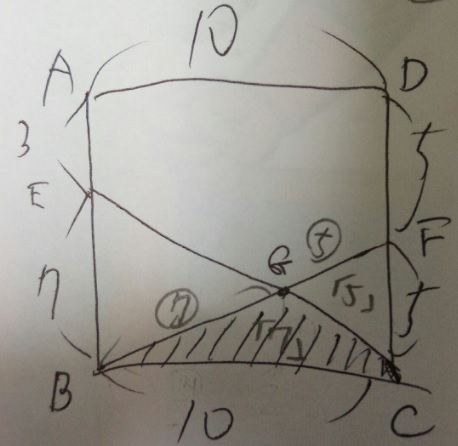
1)相似→三角形EBG7:三角形CFG5なので対応する辺FG5:BG7の比
2)高さが同じ三角形の面積は底辺の長さの比に比例→三角形BGC「7」:三角形FGC「5」
3)三角BCFの面積は10×5÷2=25c㎡
4)求める三角形BGCの面積は三角BCFの7/12→25×7/12=175/12=14と7/12
答え)14と7/12 (□c㎡と聞かれてるので数字で答える、もちろん「と」はいらない)
まとめ
この記事を読む前に必ず「相似+三角形のテクニック3つ!」を先に読んでください。
ポイントは「平行線+特定パターン→相似」を見抜く事です。

これは分かりやすいかと思います。平行である場合は、辺の比が移動できる
という事です。左の辺の比「1:2」が右の辺の比「1:2」と同じになります。
「三角形が重なる形(ピラミッド型)+平行→相似」という発想が大事です。

「二本の線が平行」→同位角が同じ→2角が同じなので相似の三角形

「二本の線が平行」→錯覚が同じ→2角が同じなので相似の三角形
三角形ACBと三角形ECDは相似(対応する角や辺を間違えないように!!)
(関連記事)