(「速さ」の関連記事)
(基本)流水算の解き方・コツは「上り」「静水」「下り」で分ける+線分図を書く
例題)A町とB町は90km離れています。
だろうは8時にA町を出て11時にB町
に着きました。びばりは8時30分にB町を出て
10時にA町に着きました。
(1)2人が出会ったのはA町から何kmの所ですか?
(2)2人が出会ったのは何時何分ですか?
*これを「ダイヤグラム」を使って解いてみたいと思います。
ダイヤグラムとは?
●ダイヤグラムとは「速さのグラフ」です
●縦軸に距離をとり、横軸に時間をとるのが基本です

「ダイヤグラム」のポイント1!
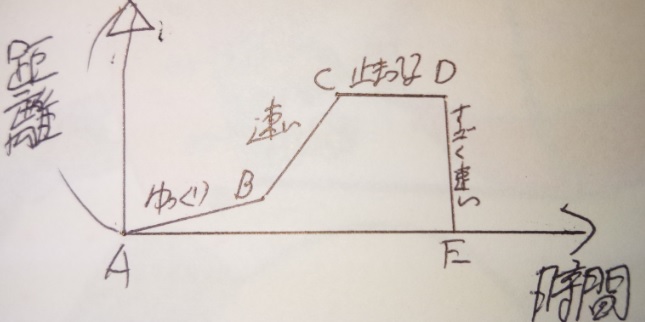
●グラフの傾きが「速さ」になります
●傾きが急なほど速いです(短時間で距離が進むわけですからね)
●時間軸(横軸)に平行なときは止まっています
ダイヤグラムの出会い算と追いつき算
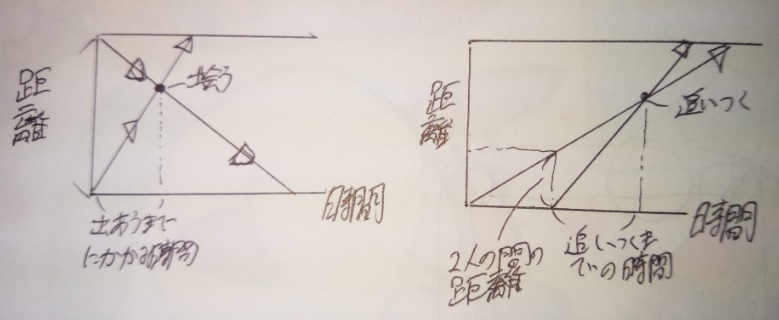
冷静に考えれば分かりますが、「出会い算」は出発地点が違います。
「追いつき算」は出発地点が同じ(事がほとんど)ですので、
ダイヤグラムを書くと以下のようになります。
では、ここで冒頭の問題を考えてみましょう。
例題)A町とB町は90km離れています。
だろうは8時にA町を出て11時にB町
に着きました。びばりは8時30分にB町を出て
10時にA町に着きました。
(1)2人が出会ったのはA町から何kmの所ですか?
(2)2人が出会ったのは何時何分ですか?
問題に思いっきり書いてありますが「出会い算」ですね?
ですので、出発地点が上と下にあるダイヤグラムになります。
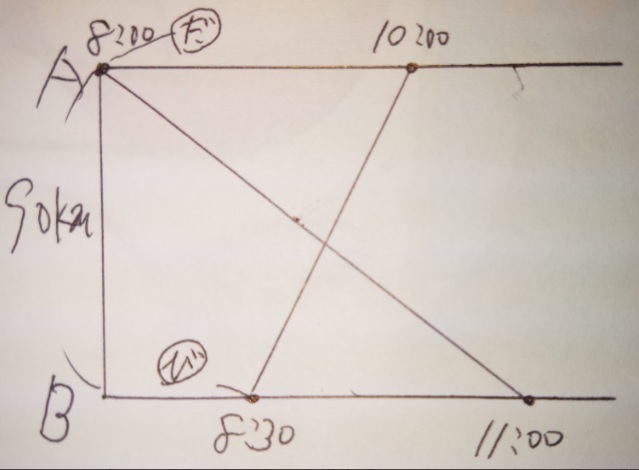
「ダイヤグラム」のポイント2!
●距離(縦軸)は、相似で(時間と)高さ(距離)の比を求める
●時間(横軸)は、(一定の距離を見つけ)速さと時間が逆比になる
時間(横)と高さ(距離)が相似(比率が同じ)になります。
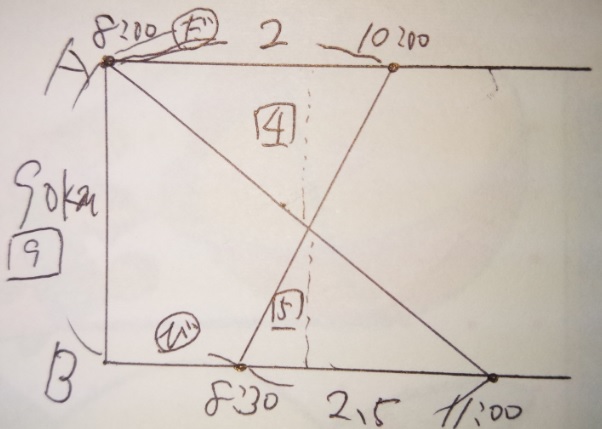
8時~10時(2時間):8時30分~11時(2時間30分)の比率は、
2:2.5→4:5
です。ですので、距離の比率も4:5で表せます。
距離はちょうど90kmですので、比率「九」と考えると、
比率「一」は10kmですね。
(1)2人が出会ったのはA町から何kmの所ですか?
答え)40km
次に、
(2)2人が出会ったのは何時何分ですか?
ですが、こちらも「相似(比率)」で出せます。

Aから2人が出会った地点までが割合「4」、そこから11時までが
割合「5」となります。全部で「9」ですね。
その時間は8時から11時までの3時間ですので180分です。
180分を「9」の割合で分けると、割合「1」は20分です。
二人が出会った地点は8時から割合「4」の地点ですから、
20×4=80分(1時間20分)
答え)9時20分
上記の問題は、
【●時間(横軸)は、(一定の距離を見つけ)速さと時間が逆比になる】
こちらでも解けます。
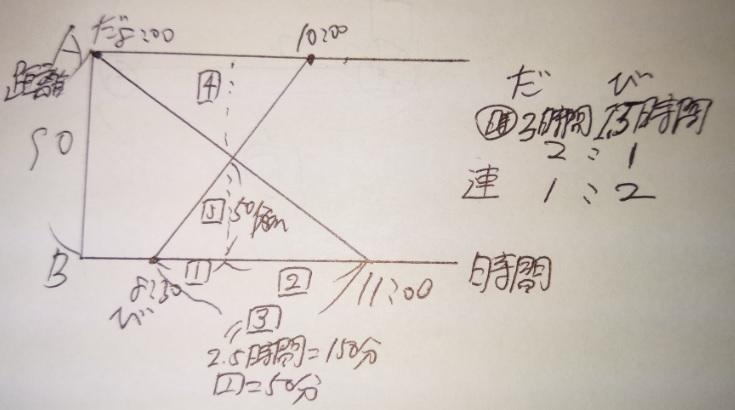
だろうは90km行くのに3時間、びばりは同じ距離を1時間半ですから、
かかった時間の比は「だろう(3)2:びばり〔1.5〕1」です。
という事は、速さは逆に(逆比)、「だろう1:びばり2」になります。
以下、上記の図の通りです。
まとめ
「ダイヤグラム」のポイント1!
●グラフの傾きが「速さ」になります
●傾きが急なほど速いです(短時間で距離が進むわけですからね)
●時間軸(横軸)に平行なときは止まっています

「ダイヤグラム」のポイント2!
●距離(縦軸)は、相似で(時間と)高さ(距離)の比を求める
●時間(横軸)は、(一定の距離を見つけ)速さと時間が逆比になる

(「速さ」の関連記事)
(基本)流水算の解き方・コツは「上り」「静水」「下り」で分ける+線分図を書く