(関連記事)
相似+三角形は(平行線+三角形の相似(ピラミッド型・ちょうちょ型))
でまとめましたが、ここでは「相似と辺の比」について考えます。
辺の比と相似のテクニック2つ!
1) 辺が分かっている三角形と相似の三角形を探す→相似比
2)1)が無理な時は補助線か延長線を引いて相似の三角形を作る
→【補助線を引いてチョウチョ型三角形の相似を作るというのが一つのパターン】
(パターンは「ピラミッド型」と「ちょうちょ型」)平行線+三角形の相似(ピラミッド型・ちょうちょ型)
1) 辺が分かっている三角形と相似の三角形を探す→相似比
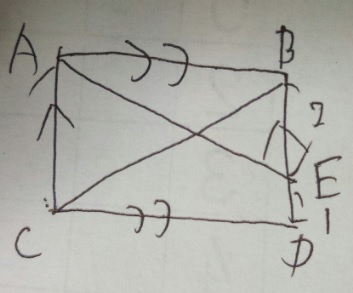
問題)平行四辺形ABCD。BE:ED=2:1のとき、AF:FEは?
(書き忘れましたが、交点をFとしてちょうだい・・・)
「二本の線が平行」→錯覚が同じ→2角が同じなので相似の三角形
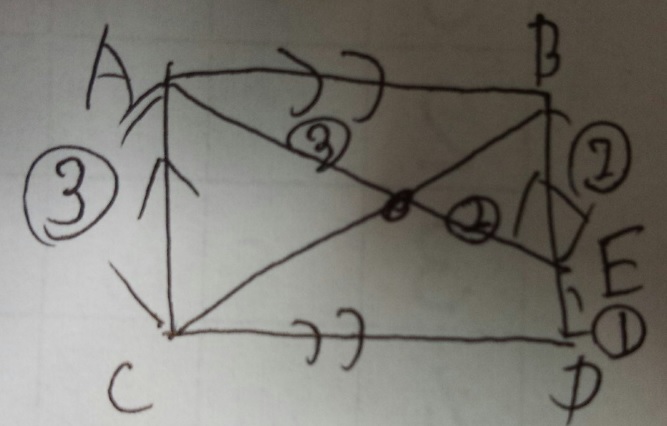
三角形AFCと三角形EFBは相似
BE:ED=2:1なので、ACは3。三角形AFCと三角形EFBは相似なので、
AF:FE=3:2 答え)3:2
1) 辺が分かっている三角形と相似の三角形を探す→相似比
これはそれなりに分かりやすいのでは?
2)1)が無理な時は補助線か延長線を引いて相似の三角形を作る
2)1)が無理な時は補助線か延長線を引いて相似の三角形を作る
こちらは多少慣れが必要かもしれませんが、先に教えておきます。
【補助線を引いてチョウチョ型三角形の相似を作るというのが一つのパターン】
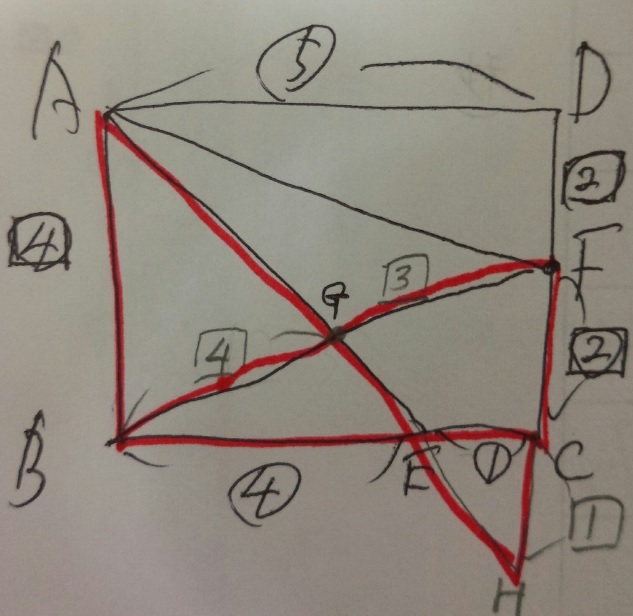
問題)平行四辺形ABCD。AE:ED1:2, DF:FC1:1です。BG:GEは?
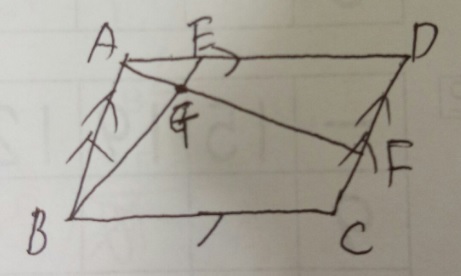
2)1)が無理な時は補助線か延長線を引いて相似の三角形を作る
ポイントは、問われている辺と関わる相似の三角形を補助線等で作るという事です。
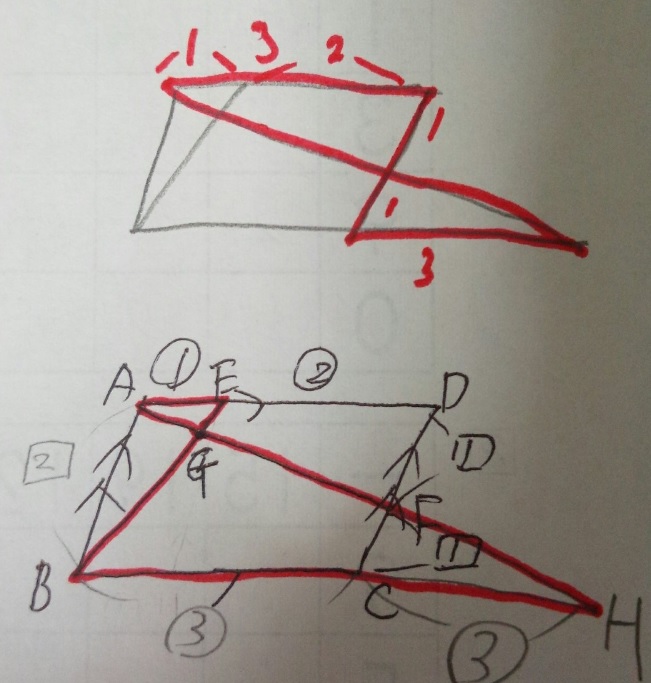
この問題の場合、上記の延長戦が引けなければ無理でしょう・・・。
1)(平行のチョウチョ型なので)三角形AEGと三角形HBGは相似
2)(上の図から分かるように)CH部分は割合③でBCと同じ。つまりBH割合⑥
3)AEは割合①なので、三角形AEGと三角形HBGの相似比は1:6
4)BG:GEは相似の三角形の対応する辺なので、6:1
答え)6:1
これは、意図的に「チョウチョ型」三角形の相似を作るパターンですね。
1) 辺が分かっている三角形と相似の三角形を探す→相似比
2)1)が無理な時は補助線か延長線を引いて相似の三角形を作る
→【補助線を引いてチョウチョ型三角形の相似を作るというのが一つのパターン】
(パターンは「ピラミッド型」と「ちょうちょ型」)平行線+三角形の相似(ピラミッド型・ちょうちょ型)
辺の比と相似のテクニック2つ!の中学入試問題等
問題)大阪桐蔭中学
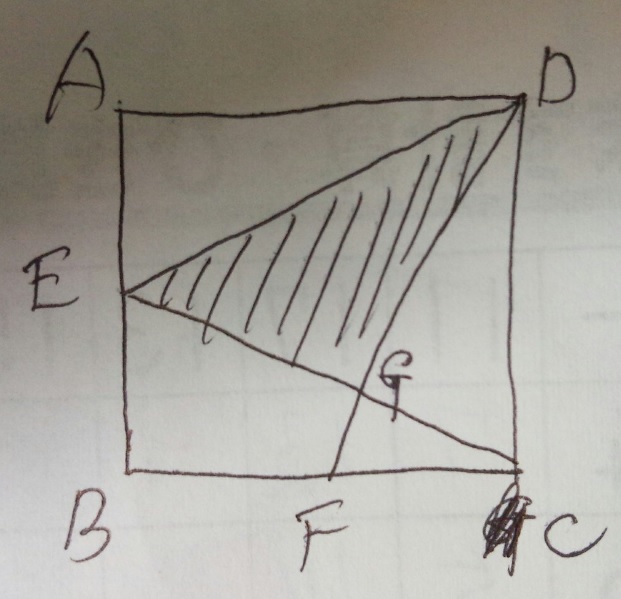
四角形ABCDは正方形。点E.Fは中点。DG:GFは?
1)補助線を引き(平行で相似の)チョウチョ型三角形作る(HGDとCGF)
2)HGDとCGFは4:1なのでDG:GFも4:1
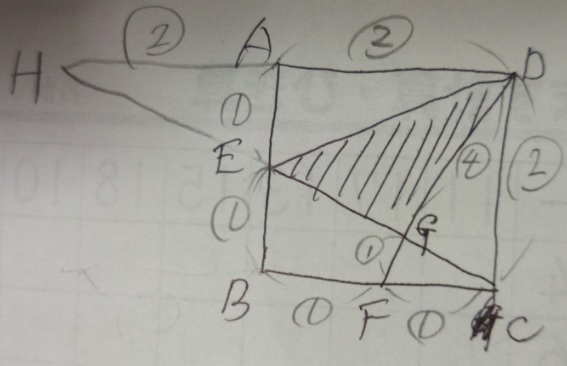
答え)4:1
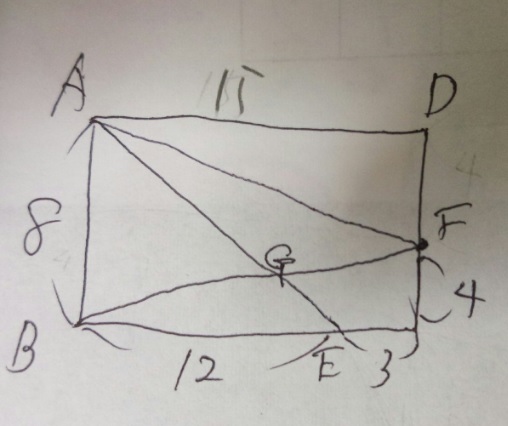
問題)明治大学付属中野中学:BG:GFをもっとも簡単な整数の比で答えてください。
【補助線を引いてチョウチョ型三角形の相似を作るというのが一つのパターン】
1)まず、それぞれの整数の比を④と「5」といった感じで最も小さい数字にしておきましょう
2)補助線を引き、チョウチョ型三角形の相似を作ります。

3)三角形ABEと三角形HCEは相似。BE「4」:EC「1」なので相似比4:1。CH「1」
4)となると三角形ABG:三角形HFGは4:3(AB4でHF3だから)
5)BG:FGも4:3
答え)4:3
まとめ
1) 辺が分かっている三角形と相似の三角形を探す→相似比
2)1)が無理な時は補助線か延長線を引いて相似の三角形を作る
→【補助線を引いてチョウチョ型三角形の相似を作るというのが一つのパターン】
(パターンは「ピラミッド型」と「ちょうちょ型」)平行線+三角形の相似(ピラミッド型・ちょうちょ型)
【補助線を引いてチョウチョ型三角形の相似を作るというのが一つのパターン】
これが非常に多いです。
(関連記事)