
(関連記事)
N進法の解き方は10進法をNで割っていき、余りと最後の商を逆から順に書く
N進法とは?
N進法は、位の上がり方がポイントです。

「N進法」とは、0からN-1までのN個の数字を使い、数がN個まとめると位が
1つ上がるような数の表し方です。
????わからね~~よ!ですよね?分かります。では「N」に具体的な数字を入れてみましょう。
我々は、「10進法」の世界に生きていますので、「N=10の10進法から」
10進法
10進法:0~9までの10個の数字を使い、数が10ずつ集まると位が1つ上がる
1の位→10の位→100の位
10進法で「10」を表すと、10です。これを説明すると、
1 0 10×1+1×0=10
10の位 1の位
2進法:コンピュータで有名
2進法:0と1の2つの数字を使い、数が2ずつ集まると位が上がる
2進法で「10」を表すと、1010(イチゼロイチゼロと読みます)です。
これを説明すると、二進法では、数が2つずつ集まると位が上がりますから、
1 0 1 0 8×1+4×0+2×1+1×0=10
8の位4の位 2の位 1の位
3進法
3進法もやってみましょう。
3進法で「10」を表すと、101(イチゼロイチ)
1 0 1 9×1+3×0+1×1
9の位 3の位 1の位

四進法と五進法
考え方は同じですので、
【四進法】
64の位 16の位 4の位 1の位
×4 ×4 ×4
【五進法】
125の位 25の位 5の位 1の位
×5 ×5 ×5
N進法のポイント
【N進法のポイント】
0)「位」はすべて「1」から始まる
1)位の上がり方がポイント:N進法のN乗になっていく
「10進法」→1の位・10¹(10)の位・10²(100)の位・10³(1000)の位・・・
「2進法」→1の位・2¹(2)の位・2²(4の位)・2³(8の位)・・・
「5進法」→1の位・5¹(5)の位・5²(25)の位・5³(125)の位
2)読み方は「10進法」以外は棒読み
101(イチゼロイチ)1010(イチゼロイチゼロと読みます)
10進法をN進法で解く方法
10進法をNで割っていき、余りと最後の商を逆から順に書く
(最後の商→余り・余り・余り・余り・・・)
素因数分解の応用編だと思ってください。
これは実際にやるのが一番です。自分で問題作って解く事もできますよね?
問題)43を3進法で表すと?
3)43
3)14・・・1↑
3)4・・・2↑
1・・・1↑
●→ →↑
余りと最後の商を逆から順に書く(最後の商→余り・余り・余り・余り・・・)
「1121」ですね。検算しましょう。
1(27の位) 1(9の位) 2(3の位) 1(1の位)
27+ 9+ +6 +1=43
問題)123を二進法で表してください
2)123
2)61・・・・1
2)30・・・・1
2)15・・・・0
2)7・・・・1
2)3・・・・1
2)1・・・・1
「1111011」
検算:1(64の位)1(32の位)1(16の位)1(8の位)0(4の位)1(2の位)1(1の位)
64+32+16+8+2+1=99+24=123
10進法をNで割っていき、余りと最後の商を逆から順に書く
(最後の商→余り・余り・余り・余り・・・)
「N進法」を使う問題になれるのがかなり大事!
この解き方はスマートではありますが、マスターしづらい場合、「N進法」
の累乗数(2・4・8・16・32・64・128)を書いていき、最大のものから
123がいくつあるか(64から始まります)を考えて、余りをさらに累乗数の
大きいものに入れていく方法もあります。

画像出典:https://www.youtube.com/watch?v=JEmfkXTRHoM
当たり前ですが、どちらでやっても答えは同じになります。
N進法で表された数を10進法で表す方法
各位の数字を正確に出せれば、これは、冷静にやって慣れると大丈夫でしょう。
問題)5進法の「132」(イチサンニ)を10進法で表すと?
~~~~~~~~~~~~~~~~~~~~~~~
【五進法】
125の位 25の位 5の位 1の位
×5 ×5 ×5
~~~~~~~~~~~~~~~~~~~~~~~~
【132】=25の位が1、5の位が3、1の位が2ですので、
(25×1)+(5×3)+(1×2)=42
25+15+2=42
N進法の中学入試問題等
上記の基本を完璧にマスターした上で、出されている問題がN進法である事に気づく必要があります。
問題)西武学園文理中学
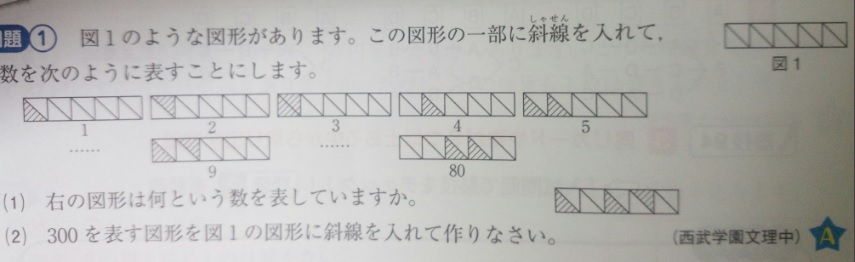
解法)(1)
1)N進法だと気づかないと解けません…。いくつ進法?
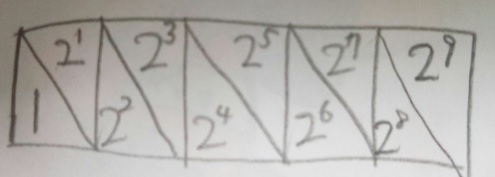
2)全てのN進法で1の位は「1」です。その後「2¹」「2²」「2³」
となっている事が分かりますでしょうか?マスに実際に書いてみるのが
良いです。【2進法】となっています。
(「4進法」と考えても、最後の計算で混乱するかもしれませんが正解は出せます)
![]()
図を数字で書くと「1の位×1」「2の位、4の位、8の位は0」
「16の位×1」「32の位0」「64の位0」「128の位1」と
なります。
128+16+1=145
解法)(2)
10進法をNで割っていき、余りと最後の商を逆から順に書く
(最後の商→余り・余り・余り・余り・・・)
2)300
2)150・・・0↑
2)75・・・0↑
2)37・・・1↑
2)18・・・1↑
2)9・・・0↑
2)4・・・1↑
2)2・・・0↑
1・・・0↑
→ →→↑
「100101100」これを図に正確に書く必要があります。
右を1の位として正確に数字を入れていきましょう。
(左が大きい位、右が小さい位ですので間違えないように)
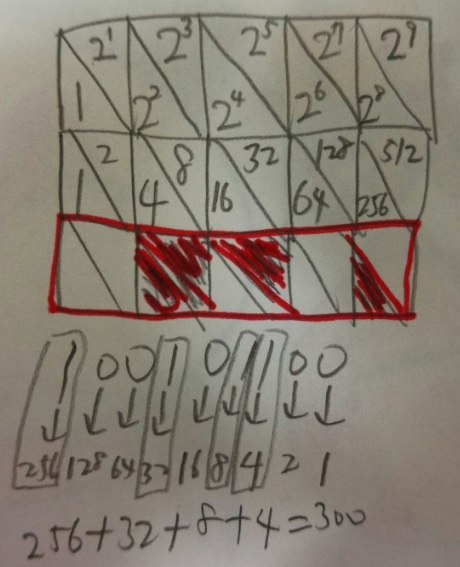
「N進法」の問題はことさら「慣れる」のが大事かもしれません。
まとめ
【N進法のポイント】
0)「位」はすべて「1」から始まる
1)位の上がり方がポイント:N進法のN乗になっていく
「10進法」→1の位・10¹(10)の位・10²(100)の位・10³(1000)の位・・・
「2進法」→1の位・2¹(2)の位・2²(4の位)・2³(8の位)・・・
「5進法」→1の位・5¹(5)の位・5²(25)の位・5³(125)の位
2)読み方は「10進法」以外は棒読み
101(イチゼロイチ)1010(イチゼロイチゼロと読みます)
10進法をNで割っていき、余りと最後の商を逆から順に書く
(最後の商→余り・余り・余り・余り・・・)
「N進法」を使う問題になれるのがかなり大事!
(関連記事)
N進法の解き方は10進法をNで割っていき、余りと最後の商を逆から順に書く