速さと比(歩幅と歩数)距離が一定→歩幅の比と歩数の比は逆比になる②
①速さが一定→距離=一定の速さ×時間。距離の比=時間の比(距離は時間に比例)
②時間が一定→距離=速さ×一定の時間。距離の比=速さの比(距離と速さは比例)
③距離が一定→一定の距離=速さ×時間。速さの比と時間の比は逆比(速さと時間は反比例)
については速さと比:「何が一定か」によってテクニックが使えますで学
びましたが、ここでは「速さと比」の『歩数と歩幅』についてまとめます。
大前提として、
歩いた距離=歩幅×歩数
です。イメージすれば大丈夫ですよね?
歩幅50cmで歩数3歩なら、50×3=150 150cm、1.5m、1m50cmです。
距離が一定→歩幅の比と歩数の比は逆比になる
問題)だろう君が5歩で歩く距離をびばりさんが6歩で歩く時、
だろうくんとびばりさんの歩幅の比は?
距離は同じなので、
「距離が一定→歩幅の比と歩数の比は逆比になる」
です。
5:6→逆比→1/5:1/6=6:5(最小公倍数の30をかけるとこの数字になります)
答え)6:5
~~~~~~~~~~~~~~~~~~~~~~~
『逆比』は大丈夫ですね?
逆比とは「逆数」の比の事です。
【逆数とは、その数にかけると1になる数】
です。2なら1/2、3なら1/3、15なら1/15ですね?
~~~~~~~~~~~~~~~~~~~~~~~~~
流水算で使う事あり!(「距離が一定→歩幅の比と歩数の比は逆比になる」)
「距離が一定→歩幅の比と歩数の比は逆比になる」
この公式、テクニックは、距離が与えられていない流水算で、上りと下りに
かかる時間の比と、速さの比が逆比になる事を使って解く事があります。
(基本)流水算の解き方・コツは「上り」「静水」「下り」で分ける+線分図を書く
問題)川沿いのA町とB町を船で往復しました。上りと下りにかかった時間の比は
5:3でした。上りの速さが時速15kmの時、川の流れの速さは?ただし、
川の流れの速さは一定とします。
1)時間の比が5:3で距離は一定です
2)距離が一定→速さの比と時間の比は逆比
3)速さの比は(5:3の逆比で)③:⑤。下りの速さは⑤
4)③:⑤=15:25なので、下りの時速は25m
5)川の流れの速さは
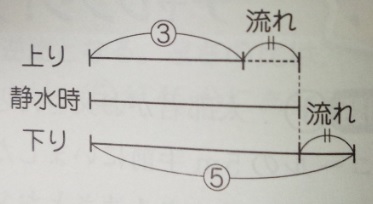
画像出典:『中学入試算数塾技100』p124
⑤ー③÷2=②÷2=①
割合③=時速15kmなので、①=時速5km
答え)時速5km
「流水算?」となった場合は、下記を読み直しておきましょう。
(基本)流水算の解き方・コツは「上り」「静水」「下り」で分ける+線分図を書く
時間が一定→速さの比=(歩幅×歩数)の比
①速さが一定→距離=一定の速さ×時間。距離の比=時間の比(距離は時間に比例)
②時間が一定→距離=速さ×一定の時間。距離の比=速さの比(距離と速さは比例)
③距離が一定→一定の距離=速さ×時間。速さの比と時間の比は逆比(速さと時間は反比例)
②時間が一定→距離=速さ×一定の時間。距離の比=速さの比(距離と速さは比例)
この部分から、
「時間が一定→距離の比=速さの比」
で、
歩いた距離=歩幅×歩数
なので、
時間が一定→速さの比=(歩幅×歩数)の比
という事になります。
問題)だろう君が3歩で歩く距離をびばりさんは4歩で歩き、だろう君
が5歩歩く間にびばりさんは6歩歩きます。だろう君とびばりさんの歩く
速さの比は?
1)歩幅の比は3:4
2)「距離が一定→歩幅の比と歩数の比は逆比になる」
3)歩数の比は4(だ):3(び)
4)時間が一定→速さの比=(歩幅×歩数)の比
なので、
(だろうの速さ)5×4:(びばりの速さ)6×3=20:18=10:9
答え)10:9
速さと比(歩幅と歩数)の中学入試問題等
問題)立教池袋中学
父が5歩で進む距離を学君は8歩で進み、1分間に父が20歩、学君は24歩
進みます。2人が同じ地点から同じ方向に出発した所、25分後に2人は102m
離れていました。(1)父と学君の速さの比と(2)学君の1歩の歩幅を求めなさい。
1)同じ距離を5歩:8歩の歩数なので、歩幅は逆比となるので父8:学ぶ5
2)歩幅が8:5で1分間の歩数が20:24なので、
時間が一定→速さの比=(歩幅×歩数)の比
より、速さの比は、(8×20):(5:24)と同じで
160:120→4:3 父と学君の速さの比は4:3
(1)4:3
時間が一定→距離の比=速さの比(距離と速さは比例)
なので、距離の比も④:③となる。時間は25分で、離れた距離は102m
なので、④ー③=① ①=102m
学君が進んだ距離は102×3=306m
歩数は(1分間に)24×25(分)=600
306÷600=0.51
(2)0.51m(あるいは)51cm
まとめ
速さと比(歩幅と歩数)は慣れないと多少混乱しそうですが、
慣れればいけるのでは?
問題をたくさん解きましょう。
①速さが一定→距離=一定の速さ×時間。距離の比=時間の比(距離は時間に比例)
②時間が一定→距離=速さ×一定の時間。距離の比=速さの比(距離と速さは比例)
③距離が一定→一定の距離=速さ×時間。速さの比と時間の比は逆比(速さと時間は反比例)
大前提として、
歩いた距離=歩幅×歩数
です。
●「距離が一定→歩幅の比と歩数の比は逆比になる」●
●時間が一定→速さの比=(歩幅×歩数)の比●
(関連記事)
速さと比(歩幅と歩数)距離が一定→歩幅の比と歩数の比は逆比になる②