(関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)
この記事では、【相似+辺の比+連比】について学ぶので先に以下の記事を読んでください。
連比の問題と解き方のテクニック3つ!youtube音声動画付き
辺の比と連比
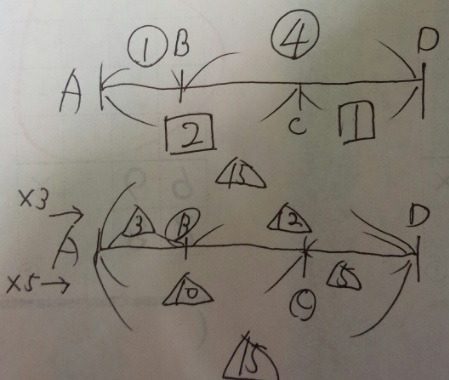
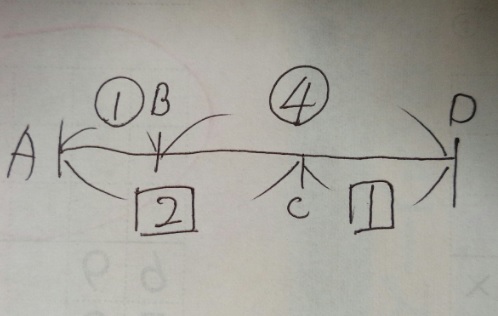
問題)AB:BD=①:④、AC:CD=「2」:「1」のとき、AB:BC:CDは?
1)共通の辺を異なる2つの比で表す
2)「連比」を使って(全体を)最小公倍数で揃えると比べられる
連比の問題と解き方のテクニック3つ!youtube音声動画付き

1)AB:BD=①:④、AC:CD=「2」:「1」ですが、ADは⑤と「3」ですね?
2)⑤と「3」の最小公倍数の【15】で揃えます(連比のテクニック)
3)AB:BD=①:④は×3(15÷5)ですね?AC:CD=「2」:「1」は×5(15÷3)ですね?
4)AB:BD=【3:12】、AC:CD=【10:5】

5)AB:BC:CD=3:7:5
答え)3:7:5
1)共通の辺を異なる2つの比で表す
2)「連比」を使って(全体を)最小公倍数で揃えると比べられる
問題)ABCDは平行四辺形。AF:FD2:3、BG:GE:EDの比率は?
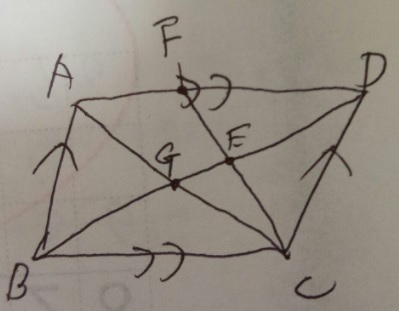
1)平行四辺形なので相似の三角形多数です
みづらい?自分で丁寧に書きなさい!
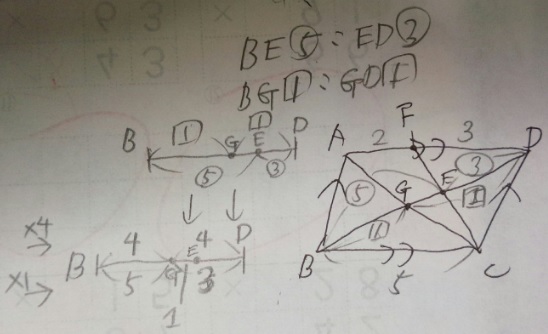
2)BG:EDは平行四辺形の対角線の交点なので「1」:「1」
3)三角形FDE③:三角形CBE③の相似なのでDE③:BE⑤
4)それを線分図に書き、最小公倍数で揃える全体が「2」と⑧なので【8】が最小公倍数

5)図の通り、BG:GE:ED=4:1:3 答え)4:1:3
この「辺の比+連比」系の問題でも「チョウチョ型」が良く出題されます。
辺の比と連比の中学入試問題等
問題)女子学院中学
ABCDは長方形。同じ印は同じ長さ。
(1)BHとIDの長さの比を最も簡単な整数の比で表すと□:□です
(2)三角形AHIの面積は□cm²
(すんません、IとBの途中のAEとの交点がHどす)
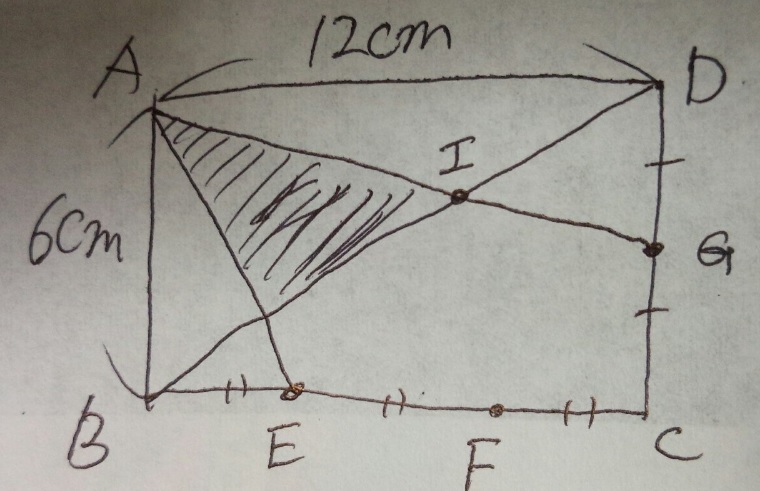
(1)BHとIDの長さの比を最も簡単な整数の比で表すと□:□です
1)共通の辺を異なる2つの比で表す→BDが使えそうですね?
2)「連比」を使って(全体を)最小公倍数で揃えると比べられる
1)チョウチョ型の相似(ABIとGDI)から、BI「6」:ID「3」→「2」:「1」
2)同じくチョウチョ型の相似(AHDとEHB)からHD⑫:HB④→③:①
3)これを線分図で揃える(連比)最小公倍数は12。BH3:HI5:ID4
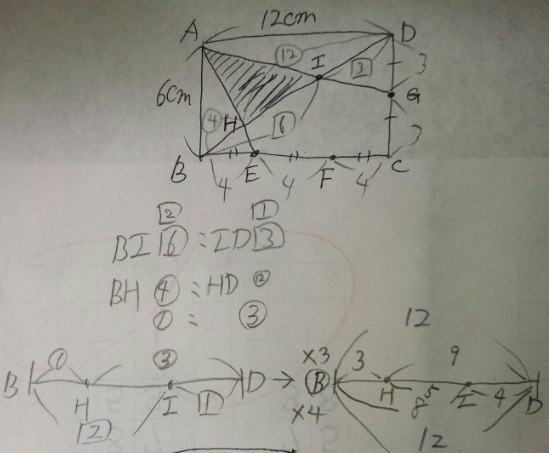
図を参照。3:4 答え)3 4
(2)三角形AHIの面積は□cm²
この種の問題ではほとんどがその前の問題(1)を使います。
1)高さの等しい三角形は底辺比=面積比
2)BH3:HI5:ID4
3)三角形ABDの面積は12×6×1/2=36cm²
4)斜線部分は底辺HI(割合が12分の5)
5)36×5/12=15 答え)15cm²
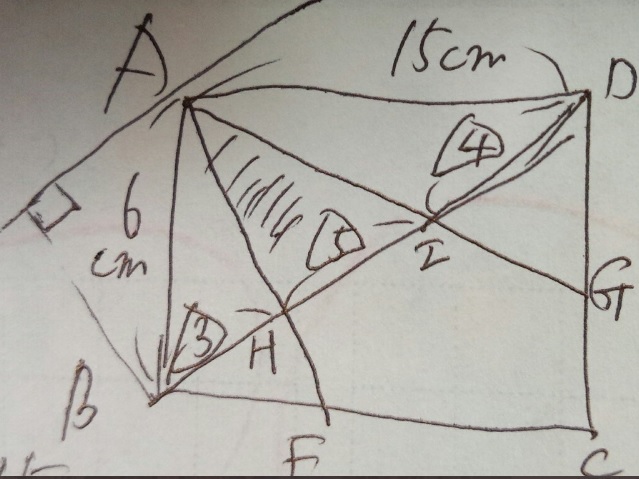
答え)(1)3 4 (2)15 (問題の聞き方が数字のみを答えさせるので単位不要)
どうでしょう?女子御三家の女子学院の問題ですが、できそうでしょ?できたのでは?
まとめ
1)共通の辺を異なる2つの比で表す
2)「連比」を使って(全体を)最小公倍数で揃えると比べられる

(関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)