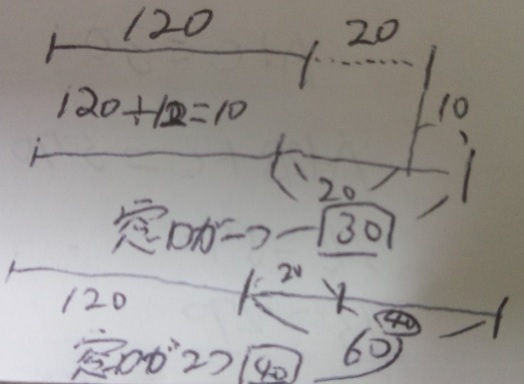
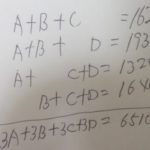ニュートン算とは?
「ニュートン算」とは、最初の数量から、一方では増え、他方では減っていく
ような状況での数量を計算する問題です。
具体的には、
(1)チケット売場で買って抜けていく客がいるのと同時に新たな客が次々と並ぶ
(2)牛が草を食べる一方で、草が生えてくる
(3)ポンプで水をくみ出す一方で水が注ぎ込まれる
こういった状況を想定してください。
例題)びばりさんは今100円持っています。今日からびばりさんは毎日10円の
おこづかいがもらえますが、毎日30円を使います。びばりさんの持っている
お金は何日目でなくなりますか(今日を1日目とします)。
(答え・解き方は下記)
ニュートン算の説き方のテクニック+基本問題
1 「4つの量」を確認
①最初の量 ②一定時間に増える量 ③一定時間に減る量 ④実質的に減る量(③-②)
2 「線分図を2本」書く
上記した例題で考えてみましょう。
例題)びばりさんは今100円持っています。今日からびばりさんは毎日10円の
おこづかいがもらえますが、毎日30円を使います。びばりさんの持っている
お金は何日目でなくなりますか(今日を1日目とします)。
1 「4つの量」を確認
①最初の量⇒100円
②一定時間に増える量⇒(1日)10円増える
③一定時間に減る量⇒(1日)30円減る
④実質的に減る量(③-②)⇒(1日)20円減る
2 「線分図を2本」書く
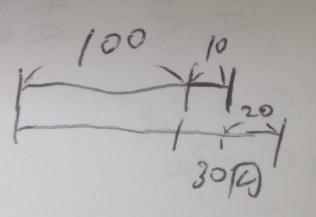
全体が100円で一日20円減るわけですから、
100÷20=5
答え)5日目
例題)120人の行列があります。さらに1分に1人ずつ行列が増えていきます。
1つの入り口で1分に2人入場させることができます。行列がなくなるのに何分
かかりますか。
1 「4つの量」を確認
①最初の量⇒120人
②一定時間に増える量⇒(1分)1人増える
③一定時間に減る量⇒(1分)2人減る
④実質的に減る量(③-②)⇒(1分)1人減る
2 「線分図を2本」書く
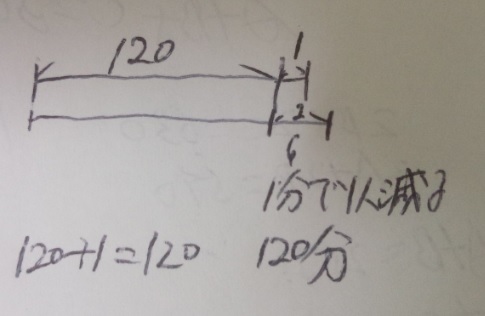
答え)120分
1 「4つの量」を確認
①最初の量 ②一定時間に増える量 ③一定時間に減る量 ④実質的に減る量(③-②)
2 「線分図を2本」書く
上記が「ニュートン算」を解くテクニックではありますが、
中学受験の算数の問題などになると、素直に「最初の量」
が分からないもの等が出てきます。
ですので、「4つの量」をいかに出すかといった思考法
が大事になってきます。
(まあ、まずは基本からですが)
ニュートン算の応用問題+中学受験問題等
例題)チケット売場の前に120人の客が1列にならんでいます。さらに毎分20人
の割合で客がその列に加わっていきます。いま、このチケット売場の1つの入り口
で売り続けると、列がなくなるまでには12分かかります。はじめから2つの入り口
から客を入れると列がなくなるまでには何分かかりますか。
例題)(四天王寺中学校)
一定の割合で水が流れこんでいるタンクがあります。このタンクが
満水のとき、毎時5㎥ の割合で放水すると30時間で空になり、毎時8㎥
の割合で放水すると12時間で空になります。このとき
次の問に答えなさい。
(1)タンクに流れこんでいる水の量は毎時何㎥ ですか。
(2)このタンクが満水のときに、毎時7㎥ の割合で放水すると何時間でタンクが空になりますか。
まとめ―ニュートン算の解き方は「4つの量」+「線分図を2本」書け!(文章題)
1 「4つの量」を確認
①最初の量 ②一定時間に増える量 ③一定時間に減る量 ④実質的に減る量(③-②)
2 「線分図を2本」書く
既に書きましたが、実際の中学入試問題では、多く(ほとんど)の場合、
「4つの量」
(①最初の量 ②一定時間に増える量 ③一定時間に減る量 ④実質的に減る量(③-②))
が素直には与えられていません。ただし、工夫をする事によって必ず「4つの数字」が
出せる(もしくはそれが答え)になっています。必ずです。
何しろ「算数」の問題ですから。
決して、「(ある特定の)人の心」のように永遠に分からない
ものではありません。最初は分からなかったとしても、何度も
解き方を見ていれば分かってくるはずです!
その際には、やはり「線分図を2本(たまには3本以上)書く」
というのがもっともニュートン算を理解しやすいでしょう。
(関連記事)