おうぎ形の面積の求め方2つと葉っぱ(レンズ)形の面積の求め方3つ!
ひもを巻きつけた図形・円の長さは「直線」と「曲線」に分ける!
問題)下記の図は、半径5cmの円が接していて、まわりにひもをか
けました。ひもの長さは何cmですか?円周率は3.14とします。
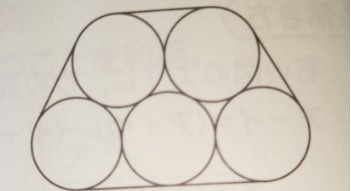
出典:『塾技100算数』p76
考え方が分からないと厳しいかと思いますが、意外とシンプルに
解けます。集中して下記を読んでいってください。
1 直線部分(長方形)と曲線部分(おうぎ形)に分ける
2 曲線部分(おうぎ形)は1つの円の円周と同じ
これがテクニックです。必ず実際に図に書き込みましょう。
ひもを巻きつけた図形・円の長さは「直線」(長方形)と「曲線」(おうぎ形)に分ける!
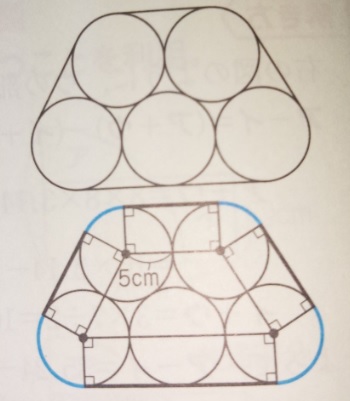
出典:『塾技100算数』p76
複数の円がまとまっていて、その周りをひもが巻きついている図形、
これよく出題されます。一見???ですが、解き方は意外とシンプルです。
1 直線部分(長方形)と曲線部分(おうぎ形)に分ける
2 曲線部分(おうぎ形)は1つの円の円周と同じ
これで解けます。

出典:『塾技100算数』p76
図の中にきれいに「長方形(直線部分)」と「おうぎ形(曲線部分)」
が書けるかどうかがほぼ全てです。
円の中心から直線を引いて見るとよく分かります。
まず、「直線部分」ですが、
上段が10cm、横が左右、10cm+10cm、下段が5+10+5=20cm
合計50cm ですね?
次に「曲線部分」ですが、これは下記で理由は書きますが、
曲線部分(おうぎ形)は1つの円の円周と同じ
と覚えて良いです。円周の長さは「直径×3.14」ですから、
(5+5)×3.14=31.4
ですので、50+31.4=81.4
答え)81.4cm
意外と簡単に解けると思いませんか?
2 曲線部分(おうぎ形)は1つの円の円周と同じ
についてですが、覚えてしまっていいのですが、より分かるために、
集中して以下の説明を読んでください。たぶん分かると思います。
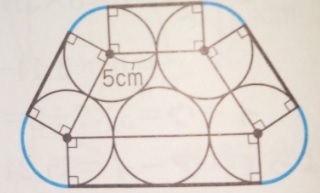
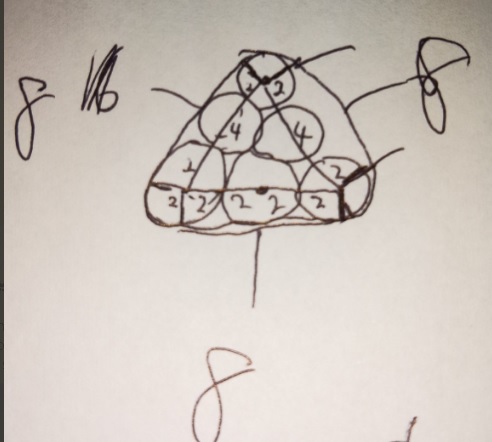
出典:『塾技100算数』p76
青の曲線部分をよ~~~くみていてください。
弧の長さの部分(青の曲線部分)の角度が全部で360度:円周と同じを証明します。
●(円4つ分)半径5cmのおうぎ形の弧ですね?
●円4つ分の角度は360×4=1440 OK?
(ここから青の曲線部分以外の角度を引いていきます)
●90度(直角)の所が(それぞれの円に2つで)8個=720度
●内側の台形に注目!台形(四角形)の内角の和=360度
まとめると、
1440度(円4つ)-720度(直角部分)-360度(台形部分)=360度
弧の長さの部分(青の曲線部分)の角度が全部で360度ですので、
弧の長さは半径5cmの円の円周と同じになります。
大丈夫ですか?

出典:『塾技100算数』p76
問題)共立女子中学
半径2cmの円6個がスキマなくっついているとします。まわりに
ひもをたるまないようにしてかけました。ひもの長さは何cmですか?
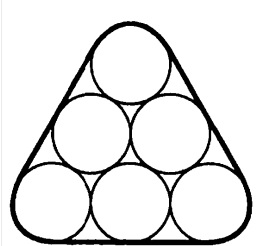
図(を書いて)にきちんと数字を書き込み、
長方形とおうぎ形に分けられましたか?
それができれば後は正確な計算だけです。
もし「よく分からない」という場合は、もう一度この記事の
冒頭から繰り返して読んでみてください。
まとめ
ひもを巻きつけた図形・円の長さは「直線」(長方形)と「曲線」(おうぎ形)に分ける!
1 直線部分(長方形)と曲線部分(おうぎ形)に分ける
2 曲線部分(おうぎ形)は1つの円の円周と同じ
おうぎ形の面積の求め方2つと葉っぱ(レンズ)形の面積の求め方3つ!
ひもを巻きつけた図形・円の長さは「直線」と「曲線」に分ける!