おうぎ形の面積の求め方2つと葉っぱ(レンズ)形の面積の求め方3つ!
ひもを巻きつけた図形・円の長さは「直線」と「曲線」に分ける!
図形の周りをひもが回っていく場合の考え方(つながれた犬が動ける面積)
図形の周りをひもが回っていく場合の考え方(つながれた犬が動ける面積)
この種類の問題は、最初は???となりますが、冷静にポイントを絞って理解しましょう。
「つながれた犬が動ける面積系」の問題のテクニック!
1 「おうぎ形」で考える(ひもは弧を描いて周る)
2 ひもを伸ばした図をきちんと書く
3 「1」「2」を忘れない
4 複数の角を曲がる場合は、半径がだんだん短くなる
(5 複数のおうぎ形を計算する時は分配算を使う)
*絶対に図を書いてください。絶対です。
問題)一辺の長さが8mの正方形の建物の角に、6mの長さのひもで
犬をつないだ場合、犬が行動できる範囲の面積は何m²ですか?
円周率は3.14です。
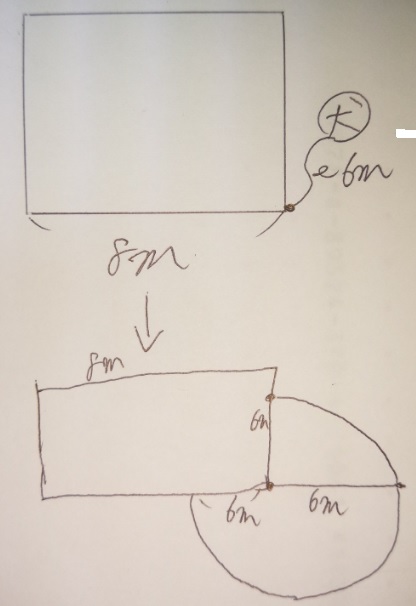
1 「おうぎ形」で考える
2 ひもを伸ばした図をきちんと書く
図のような動きが最大に動ける範囲です。図を書くと意外と
いける(解ける)気がしませんか?解けます。
●「犬が動ける範囲の面積」は、半径6mのおうぎ形です。
●6×6×3.14×3/4
(正方形なので全て90度ですから、おうぎ形の角度は360-90=270、270/360=3/4)
●36×3.14×0.75
●113.04×0.75=84.78
答え)84.78m²
問題)武蔵中学
図のような建物の角に長さ9mのロープで犬がつながれています。
この犬が動ける範囲の面積は何m²ですか?円周率は3.14です。
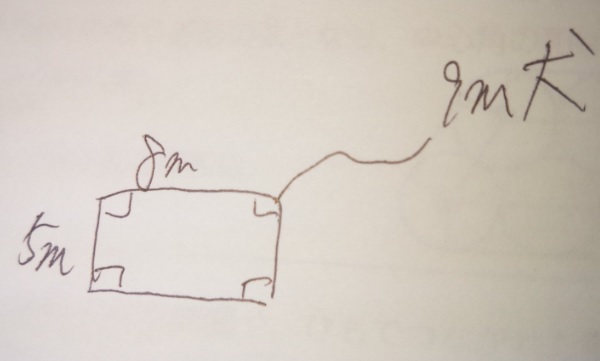
1 「おうぎ形」で考える(ひもは弧を描いて周る)
2 ひもを伸ばした図をきちんと書く
3 「1」「2」を忘れない
4 複数の角を曲がる場合は、半径がだんだん短くなる
です! やってみてください。
一回で分からなければ数回やってみてください。それにしても、
計算が大変ですね。分配法則を絶対にマスターして使いましょう。
問題)浅野中学
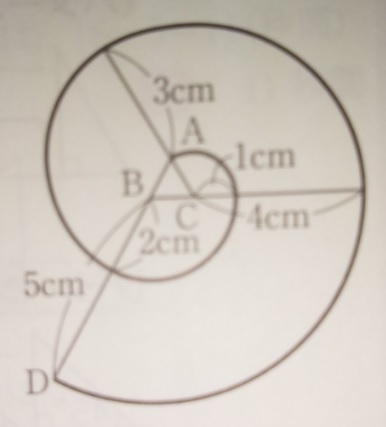
図1の三角形ABCは1辺1cmの正三角形です。ひもは頂点Aについて
います。ひもの長さは6cmです。このひもを図2の状態から始めて
頂点B、頂点C、頂点Aの順にピンと張った状態で巻きつけていくとき、
ひもの先端Dが動いてできる曲線の長さを求めてください。
円周率は3.14です。
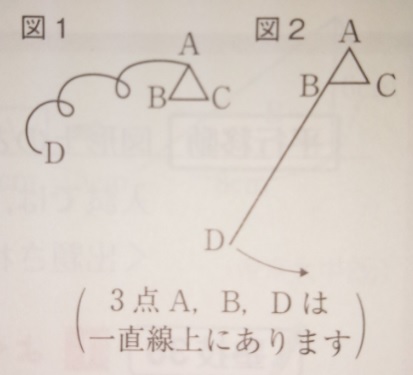
出典:『塾技100算数』p77
「つながれた犬が動ける面積系」の問題のテクニック!
1 「おうぎ形」で考える(ひもは弧を描いて周る)
2 ひもを伸ばした図をきちんと書く
3 「1」「2」を忘れない
4 複数の角を曲がる場合は、半径がだんだん短くなる
(5 複数のおうぎ形を計算する時は分配算を使う)
難しいですが、やってみてください。
複数回やってみればできるようになるのでは?
まとめ
「つながれた犬が動ける面積系」の問題のテクニック!
1 「おうぎ形」で考える(ひもは弧を描いて周る)
2 ひもを伸ばした図をきちんと書く
3 「1」「2」を忘れない
4 複数の角を曲がる場合は、半径がだんだん短くなる
(5 複数のおうぎ形を計算する時は分配算を使う)
おうぎ形の面積の求め方2つと葉っぱ(レンズ)形の面積の求め方3つ!
ひもを巻きつけた図形・円の長さは「直線」と「曲線」に分ける!
図形の周りをひもが回っていく場合の考え方(つながれた犬が動ける面積)
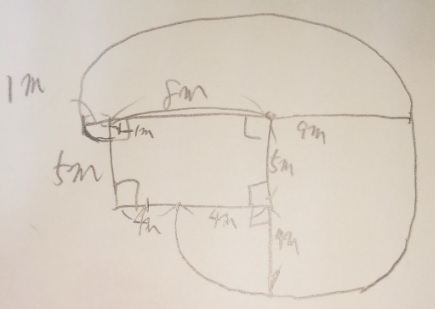 解説)9mのひもですので、建物の上の辺にピタッと伸ばすと、1m
解説)9mのひもですので、建物の上の辺にピタッと伸ばすと、1m