「ダイヤグラム」についてまだの人は先に下記記事を読んでください。
この記事は「ダイヤグラムで相似を使うパターン」について覚えましょう。
【ダイヤグラム】(縦が距離・横が時間)の基本の復習
「ダイヤグラム」(縦が距離・横が時間)のポイント1!
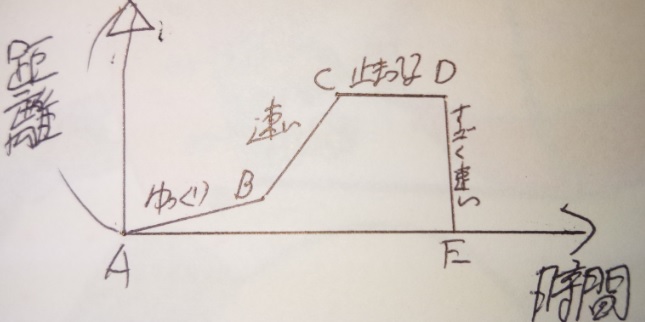
●グラフの傾きが「速さ」になります
●傾きが急なほど速いです(短時間で距離が進むわけですからね)
●時間軸(横軸)に平行なときは止まっています
「ダイヤグラム」(縦が距離・横が時間)のポイント2!
●距離(縦軸)は、相似で(時間と)高さ(距離)の比を求める
●時間(横軸)は、(一定の距離を見つけ)速さと時間が逆比になる
(関連記事)ダイヤグラムは速さのグラフ!相似・比率・逆比で読み解く
「ダイヤグラム」と「相似」のポイント
「相似」なので、当然、「比率」がポイントです。
「ダイヤグラム」と「相似」のポイント!
1)「距離」を求める時は縦軸(距離)に相似比を利用
2)「時間」を求める時は横軸(時間)に相似比を利用
*問題から分かる相似比を書き込んで解いていく
*ダイヤグラムの図+相似比が正確に書ければ90%は解けています(あとは計算)
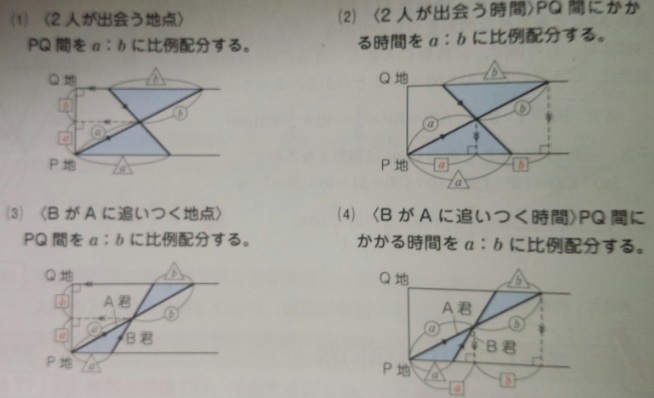
出典:『塾技100算数』p162
シンプルに言うと「ダイヤグラムを書いて、相似比を使って解く」という事ですね。
その際に「距離」であれば縦軸に相似比を、「時間」であれば横軸に相似比をもって
来るのが基本となります。それぞれの問題の条件を良く読んでください。
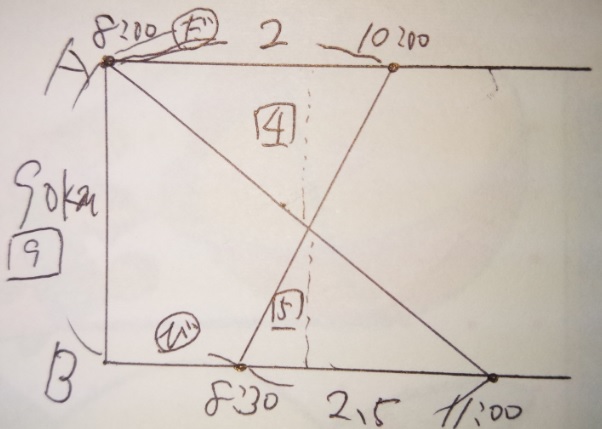
問題)だろう君の家と友達の家は120km離れています。だろう君は自分の家から、
友達は友達の家(まあ自分の家ですが混乱するので)から車で出発した所、
下記のようになりました。(1)2台の車がすれ違った時間は?(2)だろう君の家
から何kmの地点?
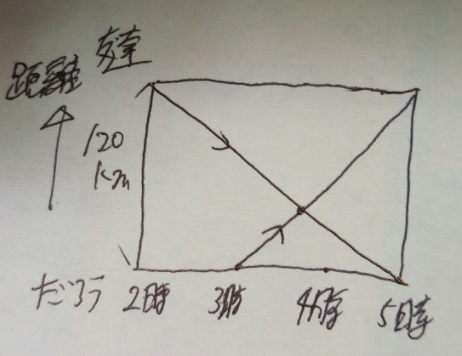
解法)
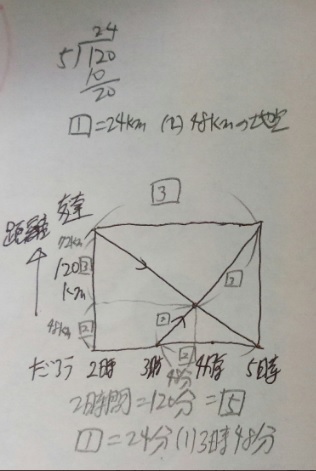
1)(時間は2時~5時の3時間なので、三角形二つの相似比は③:②
2)距離は120kmなので、これを③:②に分けると120÷⑤=24、割合①=24km
二人が出会った地点は、割合②の位置なので、だろう君の家からだと48km
(120÷2/5=48とズバッと計算しても良いです)
3)同様に、だろう君が120kmを2時間で移動しているのをすれ違う前後で分けると②:③
2時間=120分なので120÷⑤=24、①=24分
4)すれ違った場所は割合②なので48分経過している。だろう君は3時に出発しているので3時48分
答え)(1)3時48分(2)48km
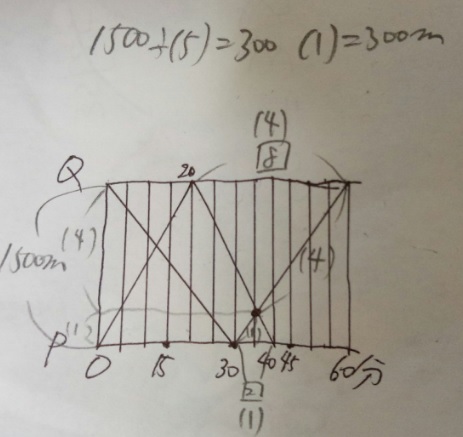
問題)1500m離れたPQ間をA君とB君が往復します。2人が2回目に会うのは
P地点から何mの地点ですか?
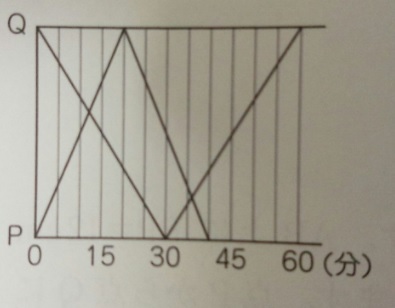
解法)(どちらがAかBかは分かりませんが、どちらでも関係ないですね)
1)グラフが重なった所が出会った場所ですね?2回目なので右側の重なりです
2)縦の線は5分刻みの時間になっています
3)分かる事(や必要な事)を図に書き込みます
ダイヤグラムの図+相似比が正確に書ければ90%は解けています(あとは計算)

4)2回目に出会った点の上下の三角形は相似で、時間軸2本(10分)と8本(40分)
が底辺部分です。ですので相似比は②:⑧=①:④
5)求めるのは距離なので縦の1500mに相似比①:④をあてはめる。
1500÷⑤=300、①=300m。2回目に出会った点は下から①の地点なのでP地点から300m
答え)300m
ダイヤグラムと相似:距離→縦軸に相似比/時間→横軸に相似比の中学入試問題等
問題)多摩大附属聖ヶ丘中学
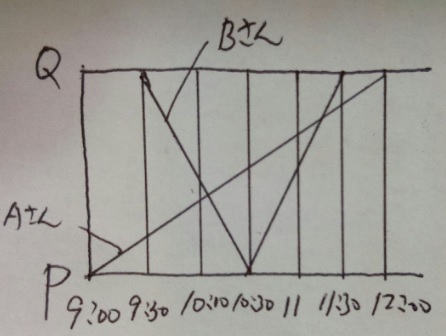
P地点とQ地点をAさんとBさんが移動しました。図を見て答えてください。
(1)AさんとBさんが最初に出会う時刻は何時何分何秒ですか?
(2)P地点から戻ってくるBさんがAさんに追いつくまでに、2人が進んだ
距離の和が200kmであるとき、P地点とQ地点の距離は何kmですか?

解法)(1)AさんとBさんが最初に出会う時刻は何時何分何秒ですか?
1)それぞれの点に適宜CとかDとか書いて見やすくします
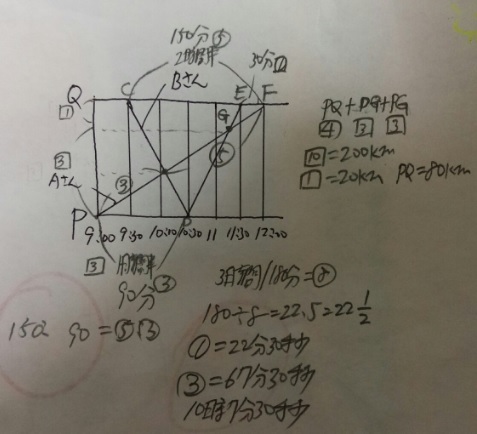
2)最初に出で会う点はCDとPFの交点ですね?
3)PDは1時間半=90分、CFは2時間半=150分。90:150=③:⑤(相似比)
4)PからFまでは3時間=180分。それが割合⑧(③+⑤)になります。
180÷8=22.5(22と1/2)。単位は分なので①=22分30秒
5)AさんとBさんが最初に出会う時刻は割合③の位置なので、22分30秒×3=67分30秒
9時から67分30秒後なので、答え)10時7分30秒
解法)(2)P地点から戻ってくるBさんがAさんに追いつくまでに、2人が進んだ
距離の和が200kmであるとき、P地点とQ地点の距離は何kmですか?
1)P地点から戻ってくるBさんがAさんに追いつくのはG地点
2)三角形EGF:三角形DGPは30分と1時間半(90分)なので、相似比「1」:「3」
3)G地点から横に点線を引き、QPを「1」と「3」に分ける(全体は割合「4」)
4)G地点までに、AさんはPGの距離を進んでいる(割合「3」)
3)G地点までに、BさんはCD(割合「4」)とDG(割合「3」)進んでいる
4)P地点から戻ってくるBさんがAさんに追いつくまでに、2人が進んだ距離の和
は割合「3」+割合「4」+割合「3」=割合「10」
5)割合「10」=200kmなので割合「1」=20km
6)PQは割合「4」なので20×4=80km
答え)80km

答え)(1)10時7分30秒 (2)80km
まとめ
「相似」なので、当然、「比率」がポイントです。
「ダイヤグラム」と「相似」のポイント!
1)「距離」を求める時は縦軸(距離)に相似比を利用
2)「時間」を求める時は横軸(時間)に相似比を利用
*問題から分かる相似比を書き込んで解いていく
*ダイヤグラムの図+相似比が正確に書ければ90%は解けています(あとは計算)

(関連記事)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(相似の関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)
体積比と相似:立体図形で相似比a:bなら体積比は(a×a×a):(b×b×b)
影と相似のポイント:太陽は平行に進む!点光源は拡がりながら進む!+横から見た図と真上から見た図!