場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る
「場合の数」+「道順(最短経路)」というのは一つのパターンになっています。
問題)図のような道路で点Aから点Bまで行く時の最短経路の数は?
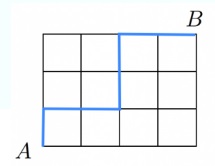
テクニックを知らないと無理っすよね?解法を知りましょう。下記で解きます。
場合の数⑥道順(最短経路問題)
★「場合の数」+「道順(最短経路)」のテクニック★
0)大前提:ある点までの行き方は1つ手前の点までの行き方の和となる
1)書き込む:地点ごとに手前の点の行き方の数の「和」を書く
2)計算する
3)問題の条件を正確に図に書き込む
0)大前提:ある点までの行き方は1つ手前の点までの行き方の和となる
0)大前提:ある点までの行き方は1つ手前の点までの行き方の和となる
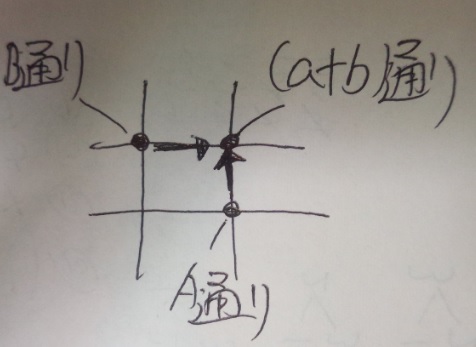
これはイメージすれば分かりますよね?
C地点にはA地点とB地点から行けるとすると、A地点まで3通りでいけて、
B地点まで2通りでいけるとすると、C地点には2+3=5通りでいけると
いうことになりますよね?
★「場合の数」+「道順(最短経路)」のテクニック★
0)大前提:ある点までの行き方は1つ手前の点までの行き方の和となる
1)書き込む:地点ごとに手前の点の行き方の数の「和」を書く
2)計算する
3)問題の条件を正確に図に書き込む
1)書き込む:地点ごとに手前の点の行き方の数の「和」を書く
1)書き込む:地点ごとに手前の点の行き方の数の「和」を書く

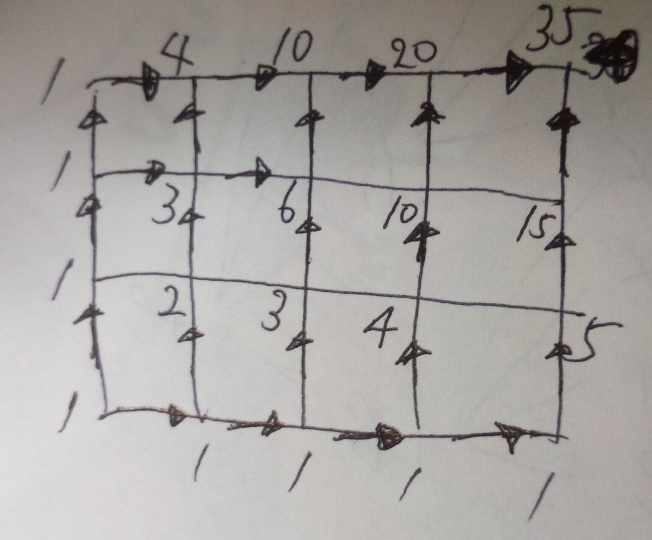
ここがポイントです。
地点ごとに手前の点の行き方の数の「和」を書く
ですから、例えば「2」の所の手前は両方1ですよね?1+1=2
「4」の手前は、1と3なので4
2つある「10」はどちらも4と6なので10になります。
慣れれば問題ないかと思います。
後は冷静に足し算をしてください。
必ず図に書き込んでください!!!
問題)図のような道路で点Aから点Bまで行く時の最短経路の数は?


答え)35通り
道順(最短経路問題)で途中どこかを通るor通らないパターン
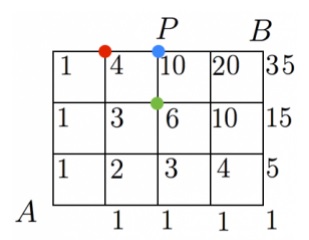
問題)AからBに行く際に必ずCを通るとすると最短経路は何通り?
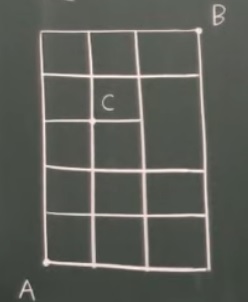
A→Bの最短経路は?系の問題に
●A→Bの途中に必ずCを通る場合の最短経路はいくつありますか●
という応用パターンがあります。その際も基本は同じですが、以下の解法になります。
道順(最短経路問題)で途中どこかを通るパターン(A→B→C)
①A→Bの最短経路数を出す
②B→Cの最短経路数を出す
③①×②が答え
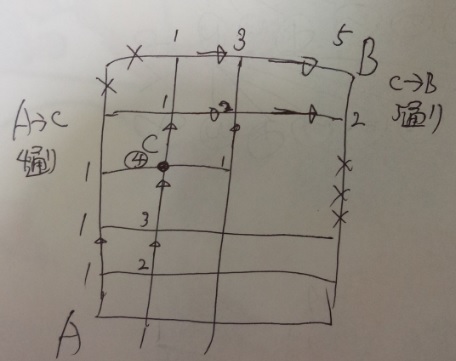
4×5=20通り 答え)20通り
ポイントは、ルートを2つに分ける事と、2つ目のルートは通らない場所が
あるので、そこは数に入れないことですかね。慣れればできるようになるのでは?
上記のような問題で、
★AからBに行く最短ルートでCを通らない経路は何通り★
という種類のモノがあります。それは、
■AからBの最短経路数-Cを通る最短経路数■
(下記の問題ですが…A→Bの最短経路数は46なので)
46-20=26 答え)26通り
また「通行止め」といったパターンもありますが、あせらずに
3)問題の条件を正確に図に書き込む
事が大事です。
場合の数:道順(最短経路問題)の中学入試問題等
問題)下図のAからBにいく最短経路は何通りありますか?
(PC上なので図は自分で書いてチョ)

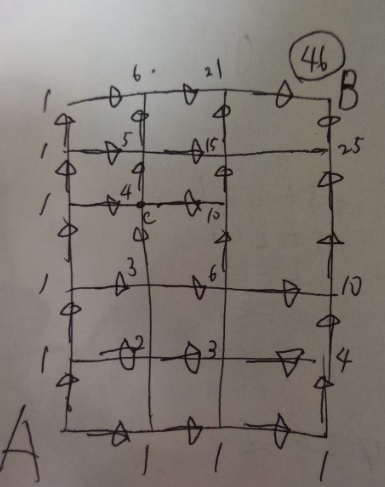
答え)46通り 必ず自分で書いてみてくださいね。
問題)明治学院中学
下図のように格子状の道があります。A地点からC地点を通って、B地点に
行く最短経路は□通りあります。
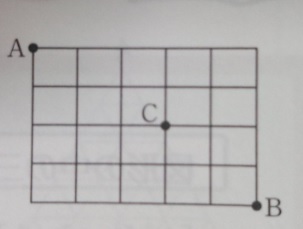
道順(最短経路問題)で途中どこかを通るパターン(A→B→C)
①A→Bの最短経路数を出す
②B→Cの最短経路数を出す
③①×②が答え
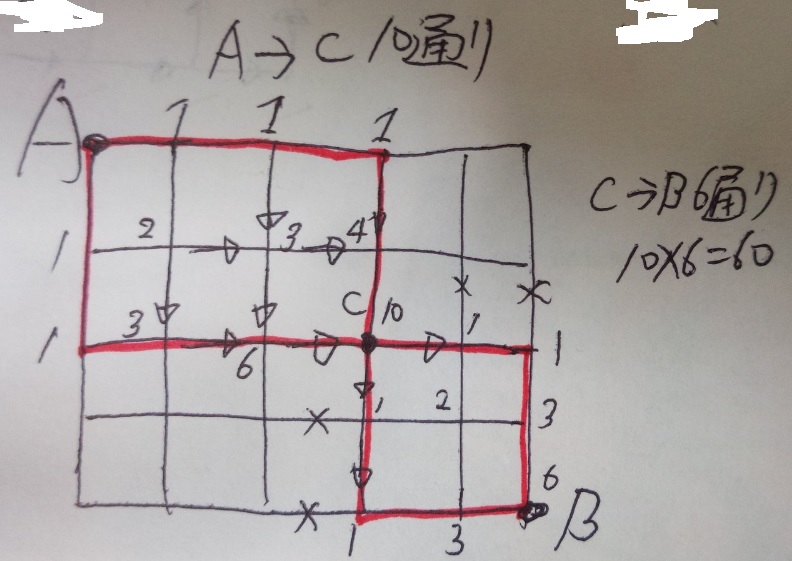
書けましたか?もしできなければ何回もやってみましょう。
答え)60 (問題が□通りとなっているので数字のみで答えます)
問題)千葉日大一中

×の道は通行止めです。A地点からB地点まで遠回りせずに行く方法は
全部で□通りです。
×部分が通れない(通行止め)という条件を踏まえて経路を書き込めば
OKです。
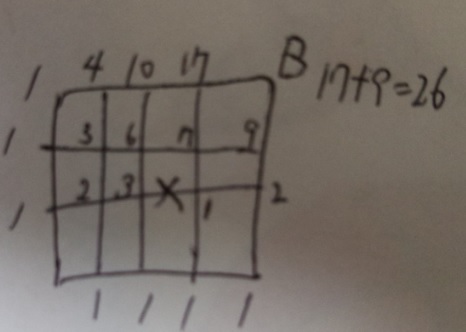
×が通れないので、3から右には行けませんので、罰の右側は1に
なります。そこだけ間違えなければ大丈夫でしょう。
答え)26 (問題が□通りとなっているので数字のみで答えます)
まとめ
「場合の数」+「道順(最短経路)」というのは一つのパターンになっています。

★「場合の数」+「道順(最短経路)」のテクニック★
0)大前提:ある点までの行き方は1つ手前の点までの行き方の和となる
1)書き込む:地点ごとに手前の点の行き方の数の「和」を書く
2)計算する
3)問題の条件を正確に図に書き込む
道順(最短経路問題)で途中どこかを通るパターン(A→B→C)
①A→Bの最短経路数を出す
②B→Cの最短経路数を出す
③①×②が答え

★AからBに行く最短ルートでCを通らない経路は何通り★
という種類のモノがあります。それは、
■AからBの最短経路数-Cを通る最短経路数■
必ず図に書き込んでください!!!
場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る