場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る
「場合の数」+図形(三角形や四角形)のパターン
問題)下図は円周上に6つの点(等間隔)を打っています。
そのうちの3点を結んで三角形を作ると何通りできますか?
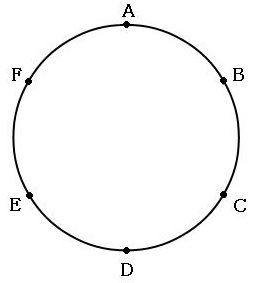
三角形や四角形といった「図形」に点を配置して、そのうちのいくつか
の点(頂点)から図形が何通りできるか?
というのが一つのパターンです。
「図形」が出てきますが、これは完全に「A個からB個を選んで組み合わせる」という
「場合の数の組み合わせ」の問題です。
場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る
問題)下図は円周上に6つの点(等間隔)を打っています。
そのうちの3点を結んで三角形を作ると何通りできますか?

(場合の数の)【組み合わせ】の考え方
●順列-ダブり部分●
(場合の数の)【組み合わせ】の公式
【A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数(順列)で割る
A個からB個を選んで並べる順列
―――――――――――――――
選んだB個の並べ方
でしたね?
【6個の点から3個の点を選んで三角形を作る】という事ですから、
【A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数(順列)で割る
A個からB個を選んで並べる順列
―――――――――――――――
選んだB個の並べ方
この公式がそのまま使えます。
6×5×4
―――― =20
3×2×1
答え)20通り
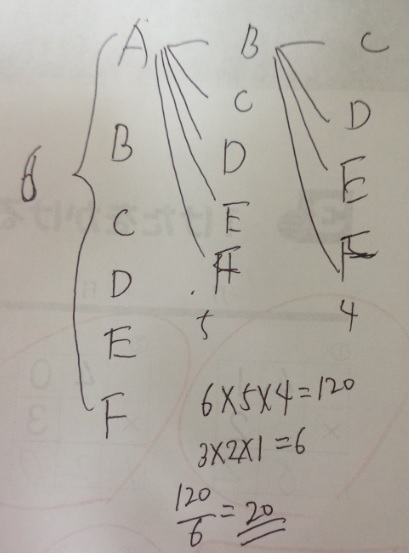
もちろん樹形図を書いても良いです。
場合の数+三角形は同じ直線上の3点を除く必要あり!
場合の数+図形で三角形の場合はちょっと注意が必要です。
場合の数+三角形は同じ直線上の3点を除く必要あり!
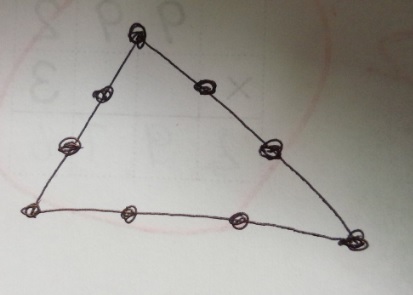
問題)上の図は三角形上に点が9個あります。3個の点を選んで三角形を
作る時、全部で何個の三角形が作れますか?
【9個の点から3個の点を選んで三角形を作る】という事ですから、
【A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数(順列)で割る
A個からB個を選んで並べる順列
―――――――――――――――
選んだB個の並べ方
この公式がそのまま使えそうですが、ちょっと注意が必要です。
同じ直線上の3点は結んでも三角形になりません(というか結べません)。
ですのでこの種の問題の場合、
場合の数+三角形は同じ直線上の3点を除く必要あり!
です。
1)点の数は9個、3個(点)を選ぶので順列は「9×8×7」
2)ダブりは3×2×1
3)504÷6=84 84通り
4)直線上の4点から3点を選ぶ場合を3つの辺すべてで引く(三角形にならない)
4×3×2÷3×2×1=4、4通りが3辺分あるので4×3=12
84-12=72
答え)72個
最初は「ん?ん?イミフ!(意味不明)」かもしれませんが、よ~く
考えれば分かるのでは?
正方形の中に正方形が何個あるかパターン
「正方形の中に正方形が何個あるかパターン」の問題があります。
★正方形の個数問題はこの式★
1)□cmの正方形の「縦の個数」×「横の個数」
2)1)を□cm、△cm、○cmと全部出して足す

(誰がどっからどう見ても全て同じ大きさの正方形です!!!1辺1cm!!!)
問題)1辺が1cmの正方形をくっつけた上記の図の中には何個の正方形がありますか?
これは解き方のテクニックを知らないと無理ですね?時間かかりすぎるし。
★正方形の個数問題はこの式★
1)□cmの正方形の「縦の個数」×「横の個数」
2)1)を□cm、△cm、○cmと全部出して足す
●1cmの正方形:縦4つ×横5つ=20
●2cmの正方形:縦3つ(1+2、2+3、3+4)×横4つ(45、56、67、78)=12
●3cmの正方形:縦2つ(123、234)×横3つ(456、567、678)=6
●4cmの正方形:縦1つ×横2つ(4567、5678)=2
20+12+6+2=40
答え)40個

辺の長さや向きで分けるパターン
(だれがどうみてもすべて正三角形です!!キリッ)
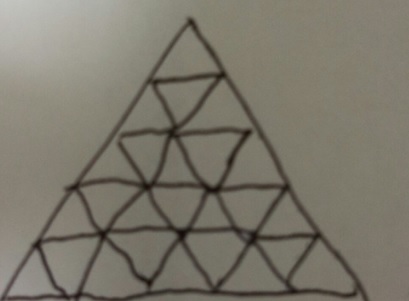
問題)灘中学(ちょっと文章だけ変えてますが問題の中身は同じです)
上の図にある正三角形は何個ですか?
こういう場合、辺の長さや向きで場合分けします。
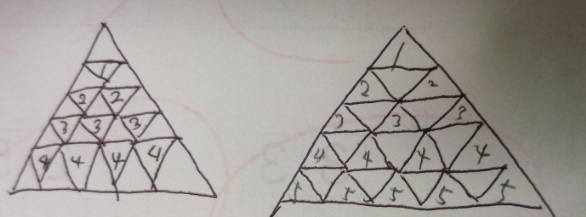
●上向きの三角形(右)と下向きの三角形(左)に分けます
●1辺の三角形:上向き15、下向き10
●2辺の三角形:上向き1+2+3+4=10個、下向き1+2=3個
●3辺の三角形:上向きのみ1+2+3=6個
●4辺の三角形:上向きのみ1+2=3個
●5辺の三角形:上向きのみ1個
25+13+6+3+1=48
答え)48個
最初はちょっと難しいと思いますが、よ~く考えて慣れていきましょう。
まとめ
三角形や四角形といった「図形」に点を配置して、そのうちのいくつか
の点(頂点)から図形が何通りできるか?
というのが一つのパターンです。
「図形」が出てきますが、これは完全に「A個からB個を選んで組み合わせる」という
「場合の数の組み合わせ」の問題です。
場合の数+三角形は同じ直線上の3点を除く必要あり!

★正方形の個数問題はこの式★
1)□cmの正方形の「縦の個数」×「横の個数」
2)1)を□cm、△cm、○cmと全部出して足す


辺の長さや向きで場合分け
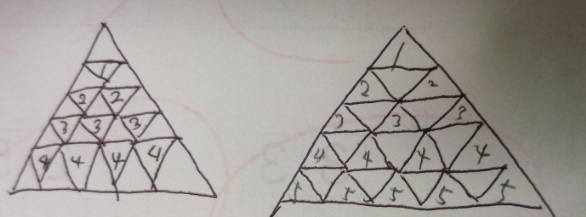
●上向きの三角形(右)と下向きの三角形(左)に分けます
場合の数③順列の公式:A個からB個選んで並べる→Aから始め1つずつ数を減らしてB個掛け算
場合の数④組み合わせの公式:A個からB個選んで組み合わせる→①順列を計算②①をB個の並べ替え数で割る