(基本)流水算の解き方・コツは「上り」「静水」「下り」で分ける+線分図を書く
「図形上の点の移動」は一見難しいですが、パターンは下記の3つ
しかほぼないので、一回マスターすればそれほど困難でもない気が
ワイはしますが・・・どうでしょうね?
「図形上の点の移動」のポイント3つ!
(●図に点の移動経路を正確に書く)
1 「旅人算」として考える
2 出発点に戻る最小公倍数で考える(スタート地点が同じ場合)
3 1回目は自力で調べる!2回目以降は最小公倍数!(スタート地点が違う場合)
図形上の点の移動のポイント
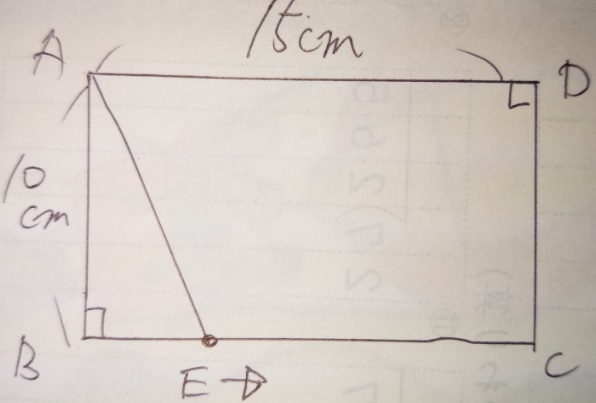
問題)下記の図の長方形ABCD上の点EはBを出発して、矢印の方向に毎秒
1cmの速さで辺の上を一周します。三角形ABEの面積が30cm²になるのは
点Eが出発してから何秒後と何秒後ですか?
「図形上の点の移動」は文字通り、図形の上を点が移動する問題です。
「図形上の点の移動」のポイント3つ!
(●図に点の移動経路を正確に書く)
1 「旅人算」として考える
2 出発点に戻る最小公倍数で考える(スタート地点が同じ場合)
3 1回目は自力で調べる!2回目以降は最小公倍数!(スタート地点が違う場合)
上記の問題であれば特殊な公式等を使わずに解けそうですね?
問題)下記の図の長方形ABCD上の点EはBを出発して、矢印の方向に毎秒
1cmの速さで辺の上を一周します。三角形ABEの面積が30cm²になるのは
点Eが出発してから何秒後と何秒後ですか?

考え方)
「三角形ABEの面積が30cm²」ですから、縦が10cmなので、横が6cmになれば
(10×6÷2=30)三角形ABEの面積が30cm²になりますね?
とすると、
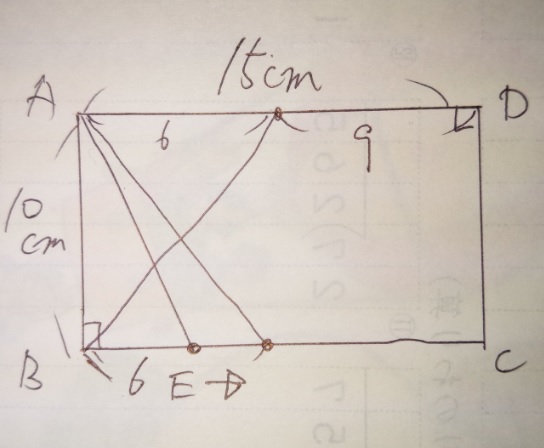
①BC間で、Bから6cmの位置になります。
もう一点は、点EがAD間にあり、
②AEが6cmの時にも三角形ABEの面積が30cm²になりますね?
①はBを出発して毎秒1cmですから「6秒後」です。
②はBを出発してDまでが25cm(25秒)で、Dから9cmの地点
までいくと、AE間が6cmになりますから、25+9=34、34秒後です。
答え)6秒後と34秒後
1 図形上の点の移動●「旅人算」として考える

出典:YouTube
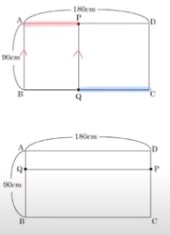
上記のような問題が典型的な「図形上の点の移動」の問題です。
直線PQが辺ABと平行になるという事は、PとQの出会い算(旅人算)
だという事が分かれば大丈夫です。
ADと平行になるというのもPとQの出会い算(旅人算)です。
(下記の図を参照)
出典:YouTube
(基本)旅人算の解き方・テクニック!―「中学受験+塾なし」の勉強法
上記記事にあるとおり、
●ニ人の進行方向が同じ場合(追いつき算)
→追いつく時間=2人の間の距離÷2人の速さの差
●二人の進行方向が反対の場合(出会い算)
→出会う時間=2人の間の距離÷2人の速さの和
です。

とすると、直線PQが辺ABと平行になるのは、
【出会う時間=間の距離(180cm)÷速さの和(秒速9cm)】
ですから、
20秒後となりますね?
20秒後に、PはAから80cmの場所、QはCから100cmの場所に
行っている事になります。

同様にADと平行になるというのもPとQの出会い算(旅人算)です。
【出会う時間=間の距離(180×2+90)÷速さの和(秒速9cm)】
ですので、450÷9=50、50秒後となりますね?
答え)①20秒後 ②50秒後
2 図形上の点の移動:出発点に戻る最小公倍数で考える(スタート地点が同じ場合)
一番最初は(多少)混乱するかもしれませんが、解法を何度も読んで、図を
じっくり見て、パターンに慣れればいけるかと思いますよ。
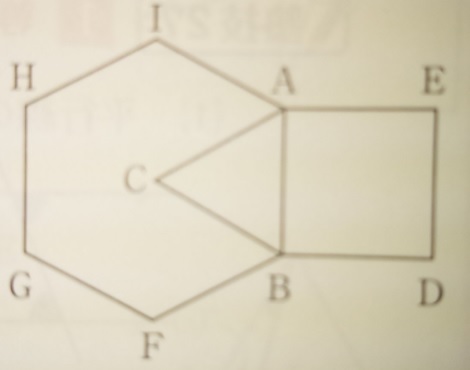
問題)帝塚山中学校
図は1辺30cmの正三角形、正方形、正六角形です、
点P、Q、Rは点Aを同時に出発して、
点PはA→B→C→A→B→・・・
点QはA→B→D→E→A→B・・・
点RはA→B→F→G→H→I→A→B→・・・
とそれぞれ正三角形、正方形、正六角形の辺上を動きます。
点Pは毎秒10cm、点Qは毎秒8cm、点Rは毎秒15cmです。
(1)点P、Q、Rが点Aで初めて出会うのは、出発してから何秒後ですか?
(2)点P、Q、Rが点Aで初めて出会うとき、点Qは図形を何周していますか?
この種の問題は「パターン化」しています。
出発点に戻る最小公倍数で考える(スタート地点が同じ場合)
これを使いましょう。
まず、「スタート地点が同じ」(点A)なので、いきなり最小公倍数を
考えましょう。また1辺がすべて30cmというのもありがたいですね?
●点Pは1辺30cmの正三角形ですから、90cmを毎秒10cmなので「1周9秒」
●点Qは辺120cmを毎秒8cmなので、「1周15秒」
●点Rは(30×6)辺180cmを毎秒15cmなので、「1周12秒」
「9 15 12」
これの最小公倍数が初めて3つの点がAで出会う時です。
「9 15 12」
3) 9 15 12
3 5 4
3×3×5×4=180
180秒後
(2)点P、Q、Rが点Aで初めて出会うとき、点Qは図形を何周していますか?
は、点Qは「1周15秒」ですから、180秒後には180÷15=12、12周していますね。
答え)(1)180秒後 (2)12周
出発点に戻る最小公倍数で考える(スタート地点が同じ場合)
3 1回目は自力で調べる!2回目以降は最小公倍数!(スタート地点が違う場合)
「2 図形上の点の移動:出発点に戻る最小公倍数で考える(スタート地点が同じ場合)」
と似たようなパターンで、「スタート地点が違う場合」は、図形上を移動する点が
1回目に出会う際には自力で調べ(る必要があり)、2回目以降は最小公倍数を使う
というパターンがあります。
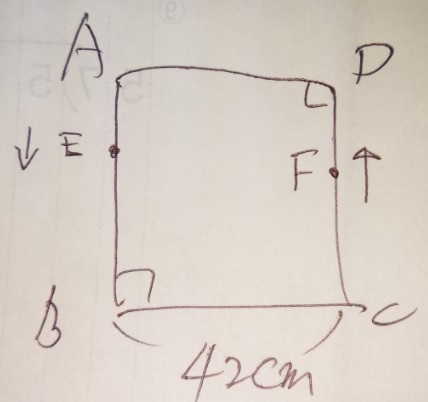
問題)1辺42cmの正方形。点EはAを毎秒7cmで出発。点FはCを毎秒6cm
で出発。それぞれ反時計回りに同時に動き始めます。点Eと点Fが5回目に
点Cを同時に通過するのは何秒後ですか?
1回目は自力で調べる!2回目以降は最小公倍数!(スタート地点が違う場合)
このパターンですね。
スタート地点が違うので、最初に点Cを通過する時には素直に最小公倍数を
使えません(それこそスタート地点が違うので)。
【点Eについて】
●点Eは毎秒7cmなので点Cを最初に通過するのは「(42+42)÷7=12秒後」
●その後は、(42×4〕÷7=24。24秒ごとに一回点Cを通過します。
【点Fについて】
●点Cを毎秒6cmでスタートするので、(42×4)÷6=28秒
●その後も28秒に一回点Cを通過します。
1回目は自力で調べる!
点E:1(12秒後)、2(12+24=36)、3(36+24=60)、4(84秒)
点F:1(28秒)、2(56秒)、3(84秒)
点Eと点Fが初めて出会うのは84秒後ですね。
2回目以降は最小公倍数!(スタート地点が違う場合)
ここからはスタート地点が同じで、スピードが違うだけなので、24秒と28秒の
最小公倍数(168秒)ごとに点Cを同時に通過します。
2)24 28
2)12 14
6 7
2×2×6×7=168秒
点Eと点Fが5回目に点Cを同時に通過するのは何秒後ですか?
が問題ですから、
1回目 84秒後
2回目 84+168
3回目 84+(168×2)
4回目 84+(168×3)
5回目 84+(168×4)=756
答え)756秒後
まとめ
「図形上の点の移動」のポイント3つ!
(●図に点の移動経路を正確に書く)
1 「旅人算」として考える
2 出発点に戻る最小公倍数で考える(スタート地点が同じ場合)
3 1回目は自力で調べる!2回目以降は最小公倍数!(スタート地点が違う場合)
「図形上の点の移動」は一見難しいですが、パターンは上記の3つ
しかほぼないので、一回マスターすればそれほど困難でもない気が
ワイはしますが・・・どうでしょうね?
(基本)流水算の解き方・コツは「上り」「静水」「下り」で分ける+線分図を書く