すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③)
回転体の見取り図の書き方!すい台の体積=すい体ー切られた部分!

展開図(直方体・立方体)に関しては、
●どの点とどの点が重なるか●
が大事です。
それ以外にもいくつかポイントがありますので、何度も読んで、
図を見て、問題を解き、慣れていきましょう。
展開図(直方体・立方体)のポイント
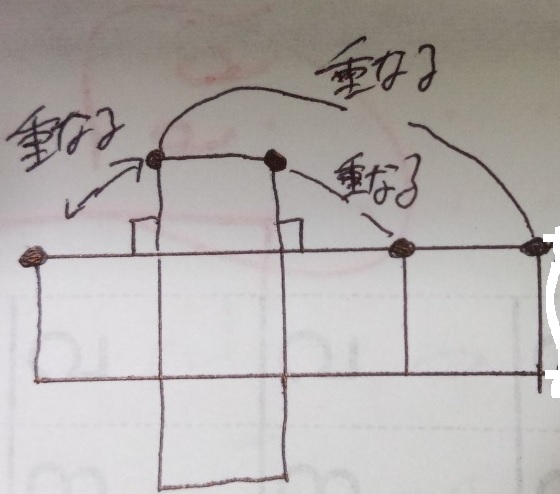
1 重なる点:展開図で90度をなす辺の頂点同士とその隣の頂点同士
2 立方体の「最も遠い点」展開図の長方形(□2つ)の対角線にくる
3 平行な辺は立体図でも展開図でも平行
4 立体図で平行な面は展開図で1つ飛ばしになる
1 重なる点:展開図で90度をなす辺の頂点同士とその隣の頂点同士

●重なる点:展開図で90度をなす辺の頂点同士とその隣の頂点同士
出典:『塾技100算数』p92
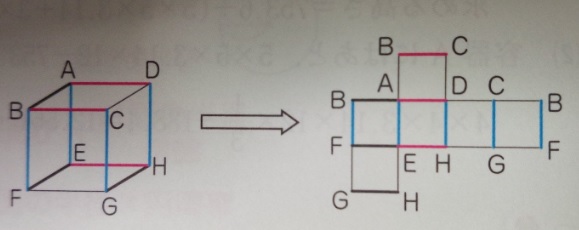
2 平行な辺は立体図でも展開図でも平行

出典:『塾技100算数』p92
●平行な辺は立体図でも展開図でも平行
AB:CD, BF:CG等々です。
3 立方体の「最も遠い点」展開図の長方形(□2つ)の対角線にくる

出典:『塾技100算数』p92
Aに対するG、Bに対するH等々です。
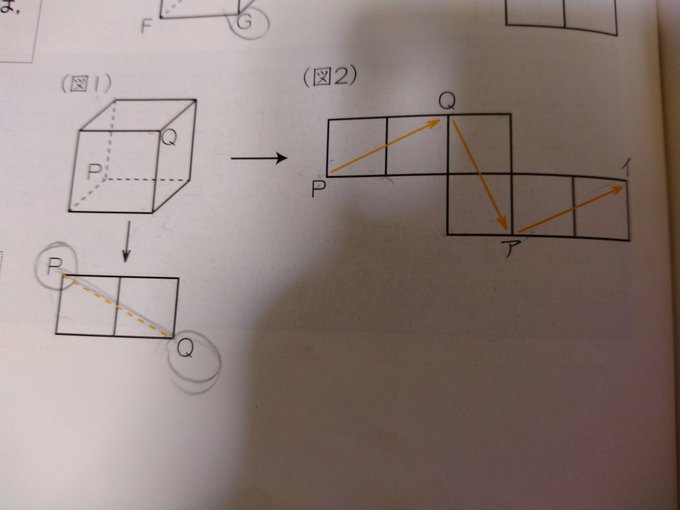
●立方体の「最も遠い点」展開図の長方形(□2つ)の対角線にくる

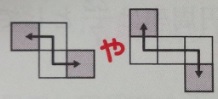
4 立体図で平行な面は展開図で1つ飛ばしになる

出典:『塾技100算数』p92
出典:『塾技100算数』p92
も立体図では平行な面になります。

出典:『塾技100算数』p92
1 重なる点:展開図で90度をなす辺の頂点同士とその隣の頂点同士
2 立方体の「最も遠い点」展開図の長方形(□2つ)の対角線にくる
3 平行な辺は立体図でも展開図でも平行
4 立体図で平行な面は展開図で1つ飛ばしになる
展開図(直方体・立方体)の問題
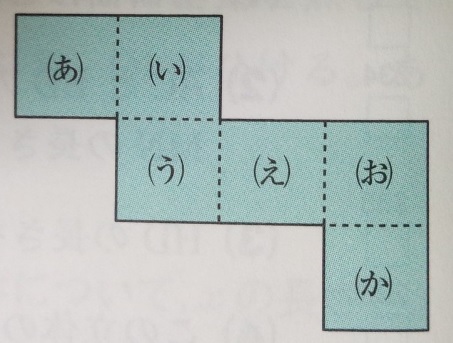
問題)
(1)下記の図は立方体の展開図です。組み立てた時(か)の面と平行に
なる面はどれですか?
(2)(う)と平行になる面は?
頭で組み立てるとおそらく中学受験の場合時間が足りなくなります。

出典:『塾技100算数』p92
も立体図では平行な面になります。
このパターンですね。
公式的にすぐに答えを出して、その上でちょっと考える程度で解きましょう。
答え)(1)(い)
(2)は
●立体図で平行な面は展開図で1つ飛ばしになる
(う)と一つ飛ばしなのは(お)
答え)(2)(お)
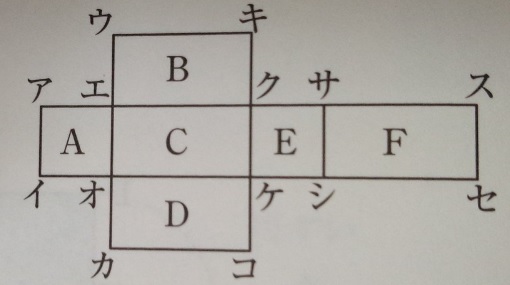
問題)武蔵野女子学院中学
下記の図は直方体の展開図です。面A、面Eは正方形で、残りの
面は長方形です。
(1)展開図を組み立てた時、面Cと平行になるのはどの面ですか?
(2)展開図を組み立てた時、点ウと重なる点はどの点ですか?
(3)全ての辺の長さを足すと64cmになります。また長方形の縦と
横の長さの比は1:2です。この直方体の体積はいくつですか?
まとめ
●重なる点:展開図で90度をなす辺の頂点同士とその隣の頂点同士
●立方体の「最も遠い点」展開図の長方形(□2つ)の対角線にくる
●平行な辺は立体図でも展開図でも平行
●立体図で平行な面は展開図で1つ飛ばしになる
すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③)
回転体の見取り図の書き方!すい台の体積=すい体ー切られた部分!