すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③)
回転体の見取り図の書き方!すい台の体積=すい体ー切られた部分!
「回転体」の問題は「すい体」と「すい台」
「回転体」の問題は「すい体」と「すい台」をまず理解しましょう。
「すい体」とは、底面と底面上にない1点を結ぶ直線全体でできる図形でしたね?
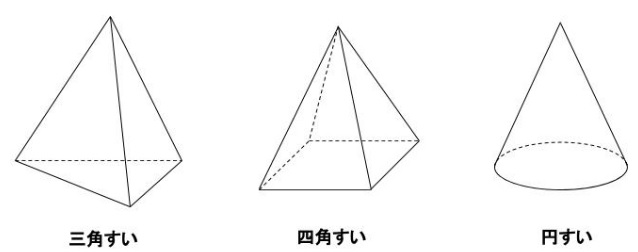
(関連記事)すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
「すい台」とは、すい体を底面に平行な平面で切ったときにできる立体です。
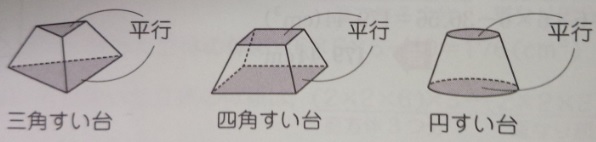
出典:『塾技100算数』p102
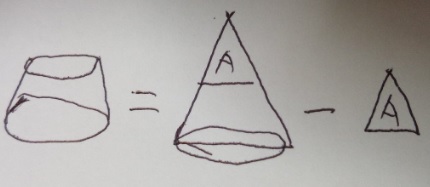
平たく言うと、「すい台」は「すい体」の上部分を(底面に平行に)切ったものです。
これが「回転体」の問題の基本となります。
すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
回転体の基本問題:すい台の体積=すい体ー切られた部分
「回転体の体積問題のパターン・テクニック」
●回転体の基本問題:すい台の体積=すい体ー切られた部分●



回転体の見取り図の描き方:平面で考える!
回転体の問題を解くには、回転体の見取り図の描き方が必須です。
与えられた図が回転したらどのようになるのか、何度も書いて、
問題を解いて慣れておきましょう。
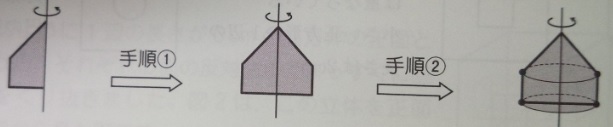
出典:『塾技100算数』p102
①回転軸に対して、線として対称(線対称)の図形を書く
②線対称の図形で、対応する2点を通る円を書く
③すると、はい、回転体の見取り図の出来上がり
上記の考え方は、「立体」を「平面」的に考えています。
・線として対象になる点を探す(線対称)
・複数の線対称を作る(点を移動)
どちらも「平面」的ですね?それぞれの線対称を円にする
という事になります。
「立体」!というと身構えがちですが、「平面」で考えればええんやで。
「むずかしいことをやさしく、やさしいことをふかく、ふかいことをおもしろく」やで。
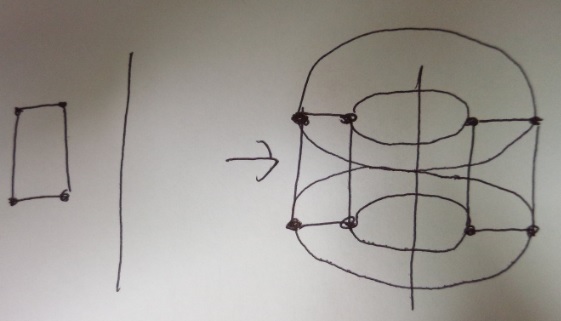
基本問題)中心の回転軸で1回転した時にできる立体図形の体積は?円周率3.14
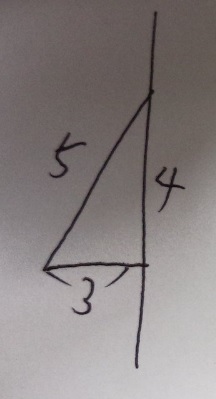
回転体の見取り図を書きます。
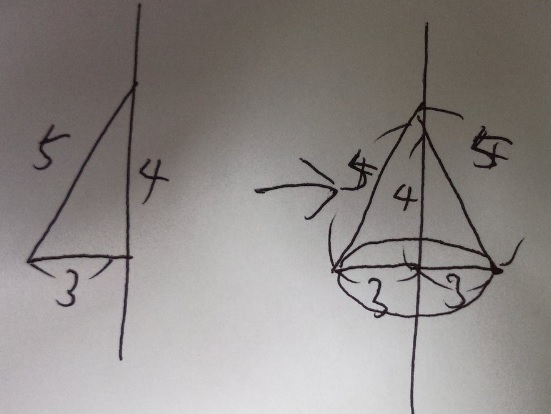
三角すいですね。
すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
すい体の体積=底面積×高さ×1/3(「体積」なので単位はcm3)
3×3×3.14×4×1/3=3×3×3.14×4×1/3=12×3.14=37.68
答え)37.68cm3
回転体のパターン
回転体で出される問題には典型的なパターンの図形があります。

出典:『塾技100算数』p102
「回転体」の問題にある程度慣れてから、再度この図をじっくり見ると、
ほぼこのパターン+その派生の問題しかないことが分かりますよ。
・回転軸と図の間に空間がある場合、空間が半径の円(円柱)の空洞ができます。
回転体の中学受験問題等
問題)下記の台形ABCDを辺CDを軸として1回転させてできる立体の体積は?
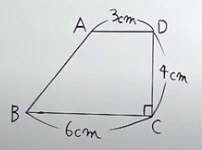
この種の問題の場合、三角形を作り、回転させて三角すいに
してしまいます。
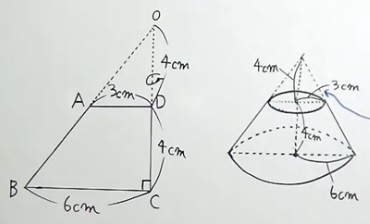
相似の考え方を使うと、でかい三角形(OBC)と小さい三角形(OAD)
の関係からOD=4と分かります。
BC:ADが2:1なので、OC:OD=2:1、OC=8なのでOD=4
そうすると、三角形OBCでBの線対称を描いて円を書くと、
右図の三角すいになります。
●回転体の基本問題:すい台の体積=すい体ー切られた部分●
(すい体の体積=底面積×高さ×1/3(「体積」なので単位はcm3))
すいたい(三角すい)の体積=6×6×3.14×8×1/3
=6×6(2)×3.14×8×1/3
=96×3.14
=301.44
切られた部分(上の三角すい)の体積
3×3×3.14×4×1/3=3×3×3.14×4×1/3
=12×3.14
=37.68
●回転体の基本問題:すい台の体積=すい体ー切られた部分●
301.44-37.68=263.76cm3
答え)263.76cm3

なお、3.14が複数回出てくるので、まとめて分配算的な式にしても
良いかと思います。
●回転体の基本問題:すい台の体積=すい体ー切られた部分●
(6×6×3.14×8×1/3)ー(3×3×3.14×4×1/3)
=(6(2)×6×3.14×8×1/3)ー(3×3×3.14×4×1/3)
=(96×3.14)ー(12×3.14)
=(96-12)×3.14
=84×3.14
=263.76cm3
問題)慶応義塾中等部
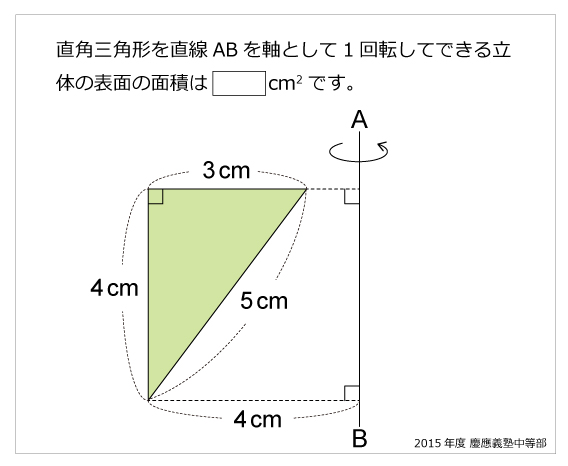
問題にはありませんが、円周率は3.14とします。
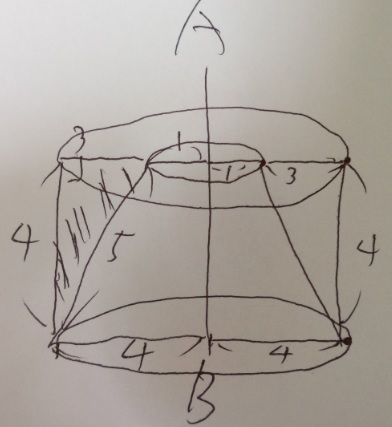
円柱の表面積から中のすい台の表面積を引いた数字になります。
●上の部分の表面積
((4×4)×3.14)ー((1×1)×3.14)
=16×3.14-1×3.14
=15×3.14=47.1
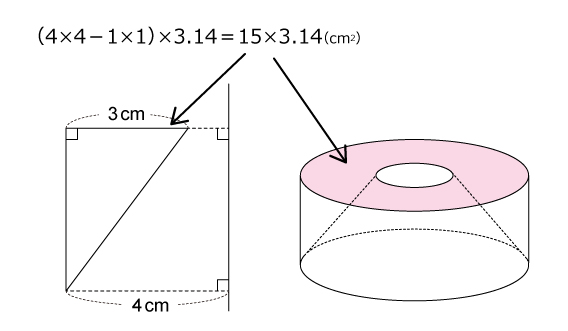
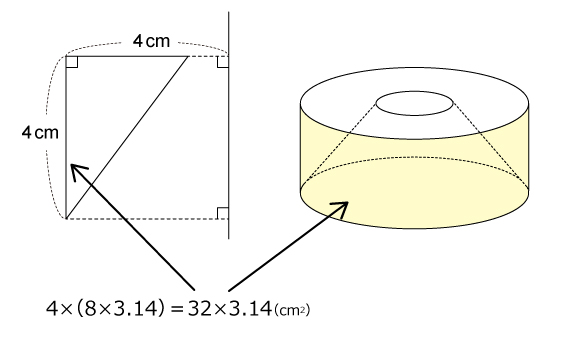
●周囲の部分の表面積
4×((4+4)×3.14)=4×(8×3.14)
=32×3.14=100.48
●円すい台の側面の面積
(2×3.14+8×3.14)×5÷2=(6.28+25.12)×5÷2
=157÷2=78.5
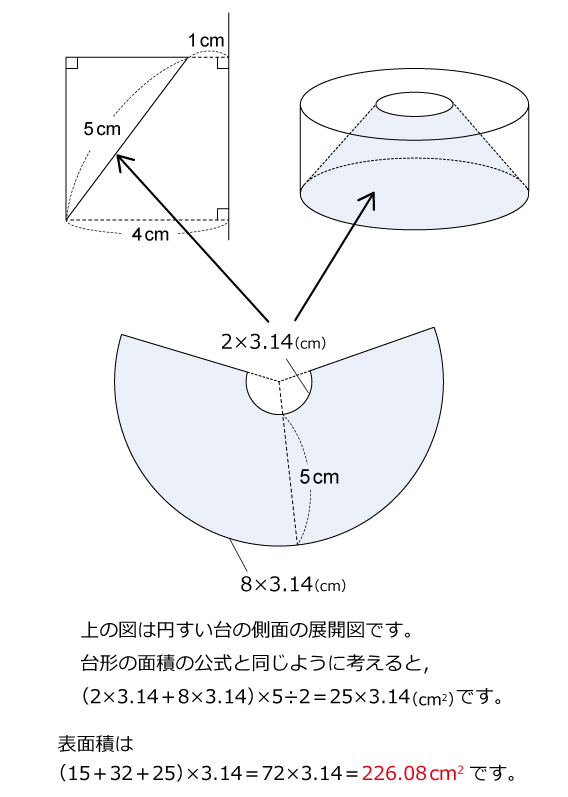
47.1+100.48+78.5=226.08
答え)226.08cm2
*この問題はかなり難しいので、6年生の最後の段階で解ければ
良いかと思います。
まとめ
「すい台」は「すい体」の上部分を(底面に平行に)切ったもの
「回転体の体積問題のパターン・テクニック」
●回転体の基本問題:すい台の体積=すい体ー切られた部分●
①回転軸に対して、線として対称(線対称)の図形を書く
②線対称の図形で、対応する2点を通る円を書く
③すると、はい、回転体の見取り図の出来上がり
上記の考え方は、「立体」を「平面」的に考えています。
・線として対象になる点を探す(線対称)
・複数の線対称を作る(点を移動)
回転体で出される問題には典型的なパターンの図形があります。

出典:『塾技100算数』p102
すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③)
回転体の見取り図の書き方!すい台の体積=すい体ー切られた部分!