すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③)
回転体の見取り図の書き方!すい台の体積=すい体ー切られた部分!
元の立方体の体積-くり抜いた立体の体積(重なりに注意)
【立方体から立体をくり抜いて体積を求める】というパターンの
問題があります。
解き方・テクニックは以下です。
●元の立方体の体積-くり抜いた立体の体積●
●くり抜く立体が重なる場合、「重なり」に注意●
(見た目のくり抜いた部分-重なり部分)=くり抜いた体積
問題)1辺の長さが6cmの立方体を、正面と横から図のように切り抜きました。
右の図は正面と横から見た図です。残った立体の体積は?
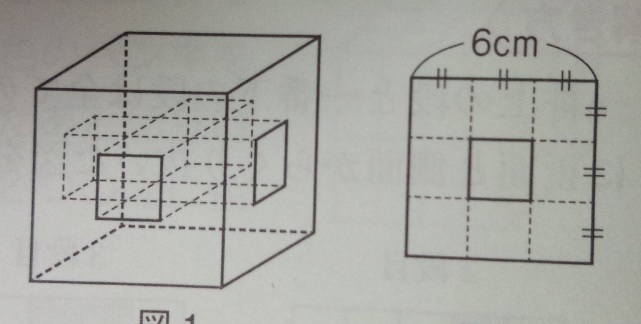
●元の立方体の体積-くり抜いた立体の体積●
●くり抜く立体が重なる場合、「重なり」に注意●
(見た目のくり抜いた部分-重なり部分)=くり抜いた体積
元の立体の体積=6×6×6=216
見た目のくり抜いた立体の体積=(2×2×6)×2=48
重なり部分の体積=2×2×2=8
重なり部分は「2回」計算していることになるので、引きます。
48-8=40(くり抜いた体積)
216-40=176
答え)176cm3
問題)鴎友学園女子中学(2010年)
1辺の長さが6cmの立方体です。図のように正面と上からそれぞれの
面の反対側までまっすぐにくりぬきました。残った部分の立体の体積は?
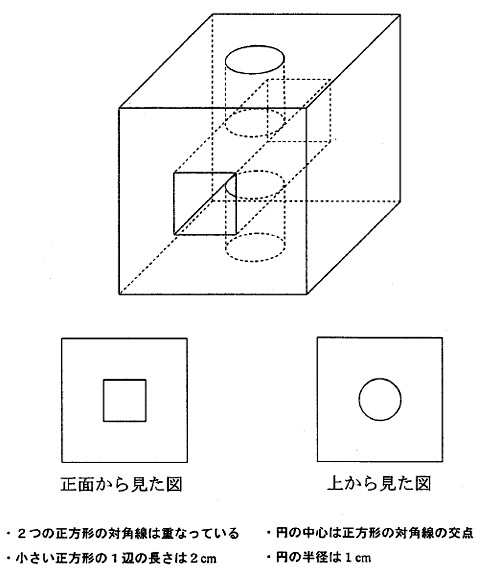
●元の立方体の体積-くり抜いた立体の体積●
●くり抜く立体が重なる場合、「重なり」に注意●
段ごとに調べる
積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③)
上記記事の
部分に書いたこととほぼ同じですが、5段程度の立方体のくり抜きの問題の
場合、「段ごと」に考えた方が良い事がよくあります。
●1段ずつに分けて、それぞれ上から見た図を描いて調べる●
問題)神戸女学院中等部 2010年
1辺が1cmの立方体を積み上げて、
図のような1辺5cmの立方体を作りました。
次に、緑の部分を反対側の面までまっすぐくりぬきます。
くりぬいた後の体積と表面積を求めなさい。
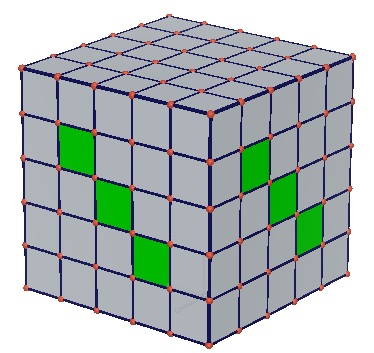
●1段ずつに分けて、それぞれ上から見た図を描いて調べる●
積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③)
上記記事の
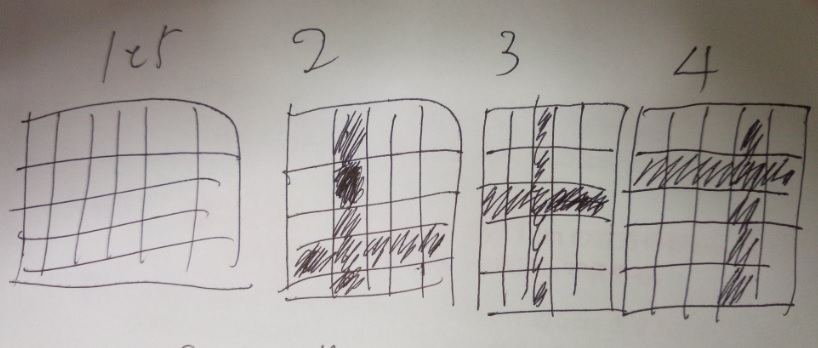
全体の体積は5×5×5=125
上から1段目と5段目はくり抜きなし。
2~4段目はそれぞれ10個くり抜かれていて、1個重なりがあるので、
9個減ります。9×3=27
1辺が1cmなので1個辺りの体積は1なので、くり抜た体積は27
125-27=98
答え)体積98cm3
表面積は
●全体-くり抜かれた表面+くり抜かれた内部の増えた表面
●全体:5×5×6面=150cm2
●くり抜かれた表面:1×1×12面=12cm2
●くり抜かれた内部の増えた表面
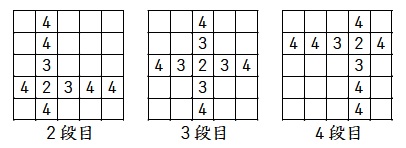
上下の段でくりぬき部分の接しているところが3cm2になり、
たてと横が重なるところが上下の面の2cm2になります。
2段目→4×6+3×2+2=32cm2
3段目→4×4+3×4+2=30cm2
4段目→4×6+3×2+2=32cm2
増えた面積→32×2+30=94cm2
150-12+94=232
答え)表面積232cm2
体積は数回でいけると思いますが、表面積は慣れないと難しい
ですね。慣れましょう。
まとめ
●元の立方体の体積-くり抜いた立体の体積●
●くり抜く立体が重なる場合、「重なり」に注意●
(見た目のくり抜いた部分-重なり部分)=くり抜いた体積
5段くらいの段ごとの立方体は
●1段ずつに分けて、それぞれ上から見た図を描いて調べる●
すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③)
回転体の見取り図の書き方!すい台の体積=すい体ー切られた部分!