すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③)
回転体の見取り図の書き方!すい台の体積=すい体ー切られた部分!
「積み重ねられた立体に色を塗る」系問題についてまとめています。
先にまとめを、
「積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!」
特に指定がなく、立方体の外側だけを塗る場合。
●3面塗りは角の8箇所
●2面塗りは3面塗りで挟まれた部分
●1面塗りはそれ以外の部分
画像出典:https://www.chugakujuken.com/koushi_blog/yoshioka/20170213.html
●1段ずつに分けて、それぞれ上から見た図を描いて調べる●


画像出典:https://www.chugakujuken.com/koushi_blog/yoshioka/20170213.html
「積み重ねた立方体に色を塗る」とは?
文字通り「積み重ねた立体に色を塗る」事です。そのままやないかい!
いや、そうですが、まずはそれをイメージしてください。

画像出典:https://www.chugakujuken.com/koushi_blog/yoshioka/20170213.html
ポイントは、
「どこが塗られて、どこが塗られないか?」
「1色、2色、3色の場所はどこか?ぬられていないのはどこか?」
です。
積み重ねた立方体に色を塗る系問題のテクニック!

画像出典:https://www.chugakujuken.com/koushi_blog/yoshioka/20170213.html
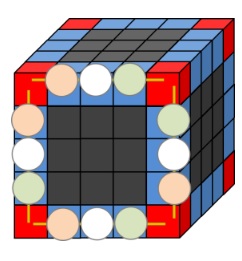
図を見ると分かりますが、特に指定がなく、立方体の外側だけを塗る場合。
●3面塗りは角の8箇所
●2面塗りは3面塗りで挟まれた部分
●1面塗りはそれ以外の部分

画像出典:https://www.chugakujuken.com/koushi_blog/yoshioka/20170213.html
これは、立方体の図に慣れる事と、実際に問題文の図を塗りつぶして
見ると分かってくると思います。
ただし、出される問題は「2面塗られている立方体の数は何個?」
といった問題なので、上記のように「どこに塗られているか」だけが
分かってもミスしやすくなります。そのために以下のテクニックを
使ってください。
●1段ずつに分けて、それぞれ上から見た図を描いて調べる●

画像出典:https://www.chugakujuken.com/koushi_blog/yoshioka/20170213.html

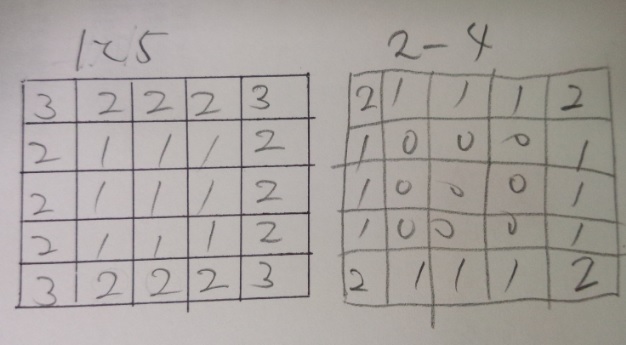
上から1列目と5列目は同じです。2~4列目も同じです。
3面塗り:4箇所×2=8 8個
2面塗り:12箇所×2=24、4箇所×3列=12 24+12=36 36個
1面塗り:9×2=18、12×3=36 18+36=54 54個
塗られていない(0):9×3=27 27個
以上が、基本となります。
あとは、問題文に応じて、きちんと
「どこが塗られているのか」を把握し、
●1段ずつに分けて、それぞれ上から見た図を描いて調べる●
という事になります。
問題)下記はすべて同じ大きさ(1辺1cm)の立方体を積み重ねてできた大きい立方体
で、大きい立方体の表面にのみ色を塗っています。
(1)小さい立方体の数は?
(2)すべてをバラバラの小さい立方体にしたら面はぜんぶでいくつ?
(3)色を塗った小さい立方体の面の数は?
(4)色を塗った面積と縫っていない面積の比は?

画像出典:https://www.chugakujuken.com/koushi_blog/yoshioka/20170213.html
(1)小さい立方体の数は?
1列に5×5=25、それが5列なので、25×5=125
(2)すべてをバラバラの小さい立方体にしたら面はぜんぶでいくつ?
立方体の数が125で、1つの立方体の面の数は6個なので、
125×6=750
(3)色を塗った小さい立方体の面の数は?
大きい立方体の1面に小さい立方体が25個、大きい立方体の面は6面。
25×6=150
(4)色を塗った面(面積)と縫っていない面(面積)の比は?
色を塗った面が150なので、塗っていない面が、
750-150=600
150:600=1:4
答え)(1)125個 (2)750(面)(3)150(面)(4)1:4
くり抜きがある場合も「段ごと」に考える
「くり抜き」がある場合も「段ごと」に考えるのポイントです。
●1段ずつに分けて、それぞれ上から見た図を描いて調べる●
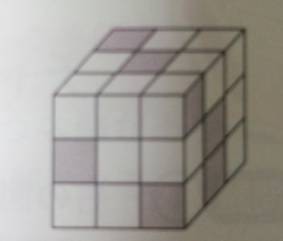
色を着けた小さい立方体を反対側までくり抜いた場合に残る小さい立方体の数は?
●1段ずつに分けて、それぞれ上から見た図を描いて調べる●

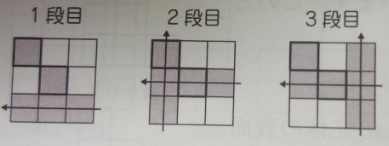
出典:『塾技100算数』p98
4+4+3=11 答え)11個
え?よく分からない?何度も図を見ていれば分かるようになると
思います。あとは問題をたくさん解く事ですね。
まとめ
「積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!」
特に指定がなく、立方体の外側だけを塗る場合。
●3面塗りは角の8箇所
●2面塗りは3面塗りで挟まれた部分
●1面塗りはそれ以外の部分
●1段ずつに分けて、それぞれ上から見た図を描いて調べる●


画像出典:https://www.chugakujuken.com/koushi_blog/yoshioka/20170213.html


出典:『塾技100算数』p98
すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
積み重ねた立方体に色を塗る系問題のテクニックは「段ごとに見る」!(積み重ねられた立体③)
回転体の見取り図の書き方!すい台の体積=すい体ー切られた部分!