(関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)
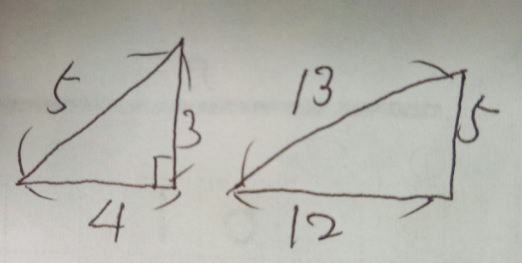
ピタゴラス数:直角三角形の基本(3:4:5)
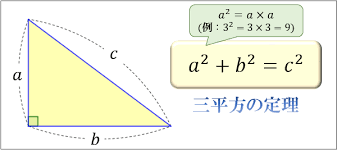
有名な「ピタゴラスの定理」(三平方の定理)は、「直角三角形に
おいて、最も長い辺の二乗は、最も短い辺と、次に短い辺の二乗の和と等しい」。
というものですね?
なお、ピタゴラス(紀元前582年~紀元前496年)は古代ギリシャの数学者、哲学者です。
さて、「中学受験+直角三角形」としては以下の点を知っておきましょう。
直角三角形の(3辺全てが整数)辺の組み合わせを【ピタゴラス数】と言います。
中学受験に良くでる【ピタゴラス数】
①3:4:5 ②5:12:13

9+16=25 25+144=169
【3:4:5】は一番有名な「ピタゴラス数」です。中学受験にも
良くでます。ただし、そのまま出るのではなく、「3:4:5」に
比例した倍数が良く出ます(「9:12:15」とか「12:16:20」とか「15:20:25」とか)。
また、「5:12:13」も良く出題されます。5×5=25、12×12=144、13×13=169
12×12=144(語呂合わせ「12月はイシシ」)
13×13=169(語呂合わせ「いざ、いちろー君!」)
直角三兄弟型の相似
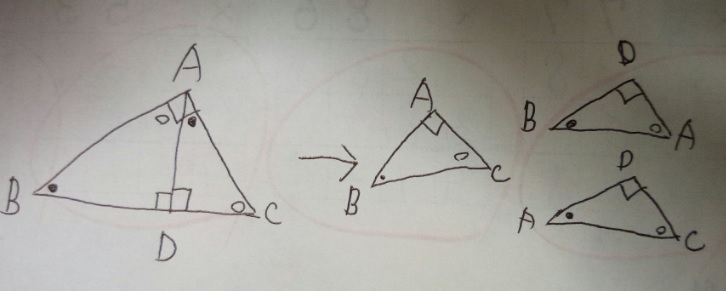
これも有名な「3つの直角三角形がすべて相似」になるというパターンです。
問題)?部分は何cmですか
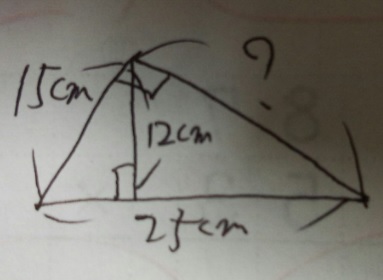
す、すいません。ABCD的なものを入れ忘れました。自分で書いて・・・。
さて、上記は有名な「直角三角形+相似」の形ですから、対応する辺の比で
出せますが、より簡単な方法もあります。まずは基本から。
1)25:15=15:□→5:3=15:9 一番小さい三角形の最も短い辺9cm
2)25-9=16、二番目に小さい三角形の二番目に長い辺16cm
3)12:15=16:?→4:5=16:20 ?=20

こんなしちめんどくさい事をしなくても、直角三角形で、
15:?:25なわけですよね?辺の比が。という事は、3:?×1/5:5ですよね?
中学受験に良くでる【ピタゴラス数】①3:4:5
?×1/5=4なので、?=20
中学受験に良くでる【ピタゴラス数】
①3:4:5 ②5:12:13

そのまま出るのではなく、「3:4:5」に
比例した倍数が良く出ます(「9:12:15」とか「12:16:20」とか「15:20:25」とか)。
直角三角形の相似の中学入試問題等
問題)大妻中野中学
直角三角形ABCを点Bを中心に、矢印の方向に90°回転させました。
円周率は3.14とします。CPの長さは何cm?分数で答えてください
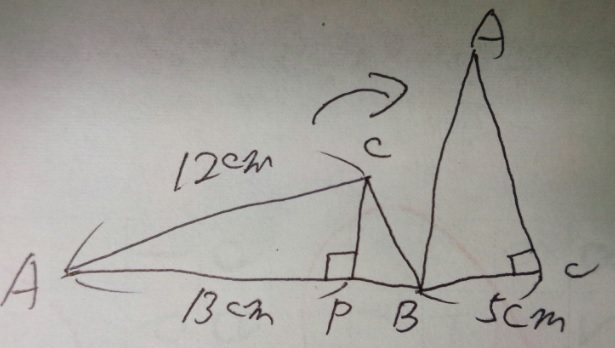
ごめんなさい…AP=13に見えますが、AB=13cmです…
CPの長さは何cm?分数で答えてください
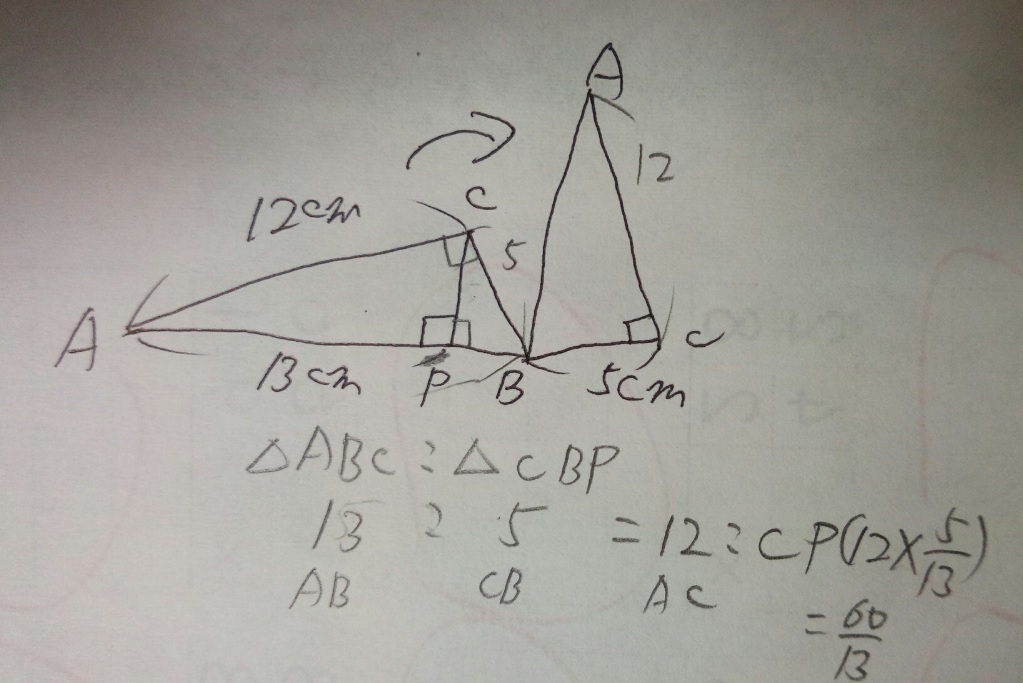
1)三角形ABCと三角形CBPは相似(2つの角度が等しいので)
2)相似比はAB13:CB5
3)CPに対応するのは、ACなので、12:AC=13:5
4)(4:1=8:?なら、8×1/4=?)なのでAC=12×5/13=60/13
5)60/13=4と8/13
答え)4と8/13cm
まとめ
中学受験に良くでる【ピタゴラス数】
①3:4:5 ②5:12:13

9+16=25 25+144=169
そのまま出るのではなく、「3:4:5」に
比例した倍数が良く出ます(「9:12:15」とか「12:16:20」とか「15:20:25」とか)。
(関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)