(関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)
相似の図形の面積比は相似比の2乗
●三角形が相似の場合、面積比は相似比の2乗と同じ●
(上記記事にも書いてあります)
この種の問題では「相似比」が聞かれているのか「面積比」が聞かれているのかに注意しましょう。
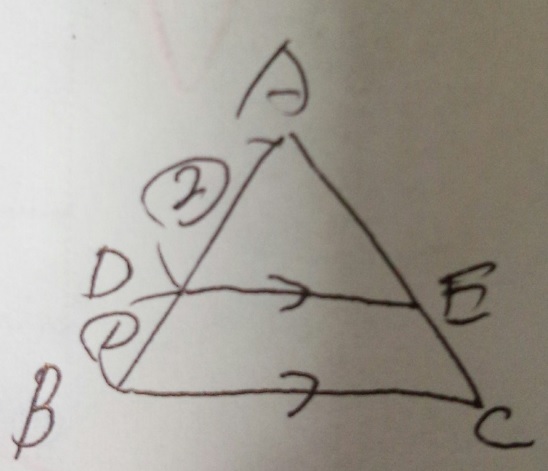
三角形ADEと三角形ABCの相似比は②:③なので、面積比は相似比の二乗です
から、(3×3):(2×2)=⑨:④となります。
また四角形DBCEの面積比も出せます。⑨ー④=⑤です。
面積比は相似比の2乗と同じは多角形でも成り立ちます。
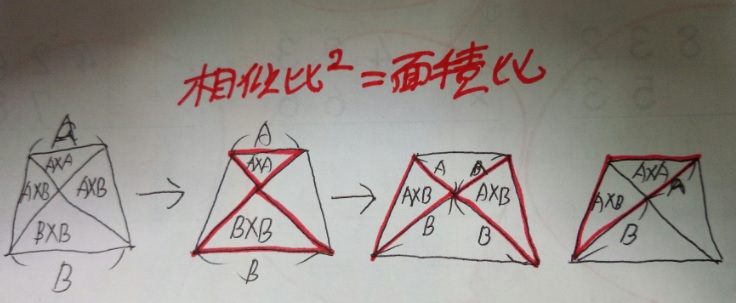
台形を三角形に分けた時の面積比のパターン
「長さ」ではなく「相似比」である事に注意してください。

この4つはパターンなので、問題を解く間に覚えてしまいましょう。面積比は相似比の2乗
問題)台形ABCDと三角形ABEの面積比は?
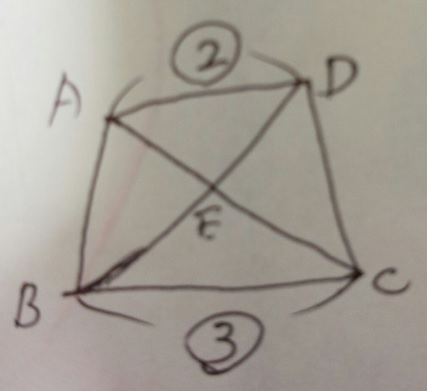
1)台形なので1組は平行です。ここでは上下ですね。なのでAEDとBECは相似
2)台形の「4パターン」から、相似比の二乗=面積比で以下の図になる
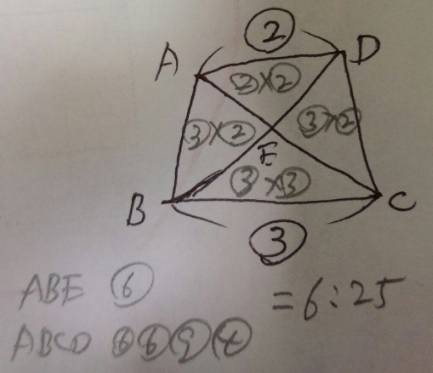
答え)25:6
面積比と相似:図形の面積比は相似比の2乗の中学入試問題等
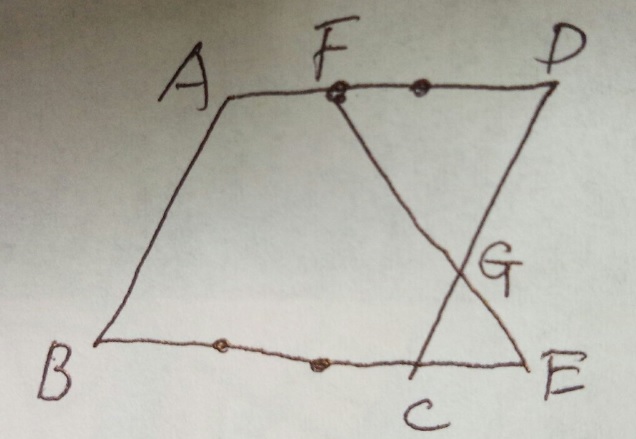
問題)大妻中学
平行四辺形ABCDです。BCを1/3伸ばした点がEです。ADを1/3に縮めた点がFです。
台形ABEFと三角形FGDの面積比を最も簡単な整数の比で表してください。
(以下は一つの解き方です。もちろん別の解き方でも論理的に正しく正解になっていればOK)
1)分かる事を図に書き込みます
2)平行四辺形なのでFDGとECGは相似。相似比は2:1なので面積比は④:①
三角形が相似の場合、面積比は相似比の2乗
3)ACに補助線を引きます。三角形FDGとADCは相似。相似比2:3なので面積比④:⑨
4)台形ABCDはADC×2なので台形ABCDの面積比は⑱
5)ABEF=ABCGF+CGE①、ABCGF=ABCD⑱ーFDG④=⑭、ABEF=⑮(⑭+①)
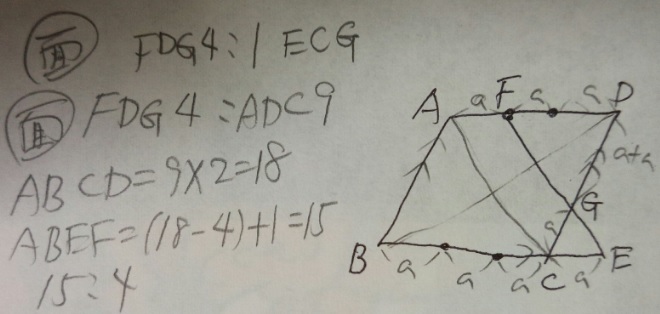
台形ABEFと三角形FGDの面積比を最も簡単な整数の比で表してください。
答え)15:4
まとめ

三角形が相似の場合、面積比は相似比の2乗
(関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)