(関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)
「折り返しと相似」のポイントは以下です。
1 「合同」と「相似」に注目
2 折り返してできる三角形はすべて相似(対応する角、辺などを書き込むこと)
折り返しと相似の基本
問題)1辺9cmの正方形です。薄い色の部分の面積は?
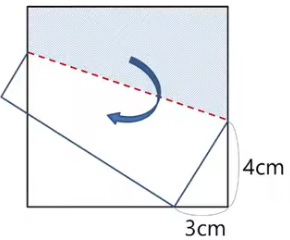
出典:https://www.youtube.com/watch?v=HZHANCrXsfQ
こんな感じのものが「折り返しと相似」の基本となります。
「折り返しと相似」のポイントは以下です。
1 「合同」と「相似」に注目
2 折り返してできる三角形はすべて相似(対応する角、辺などを書き込むこと)
問題)1辺9cmの正方形です。薄い色の部分の面積は?

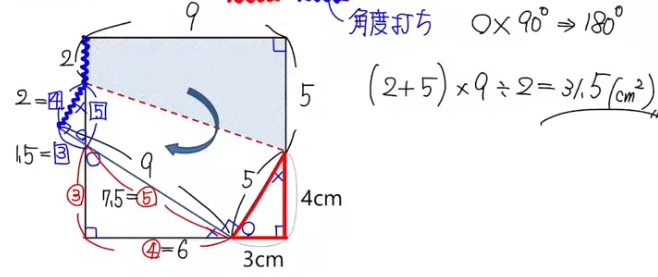
出典:https://www.youtube.com/watch?v=HZHANCrXsfQ
1)折り返した部分が薄い色の部分です(合同)
2)右下の三角形と左に(ちょこんと)はみ出た三角形と、左下の三角形は相似
(直角+○+×=180°で、右下の三角形をそのように設定すると、左下の×が決定できるので)
折り返してできる三角形はすべて相似
3)相似の三角形なので相似比ですべての三角形の辺が出せます(慣れれば大丈夫でしょう)

なお、このパターンでは、中学受験に良くでる【ピタゴラス数】3:4:5がよく出ます。
(関連記事)直角三角形の相似(「3:4:5」「5:12:13」)
ポイントは折り返してできる三角形はすべて相似!
この点を暗記ではなく、理屈・論理で説明できるようにしてください。
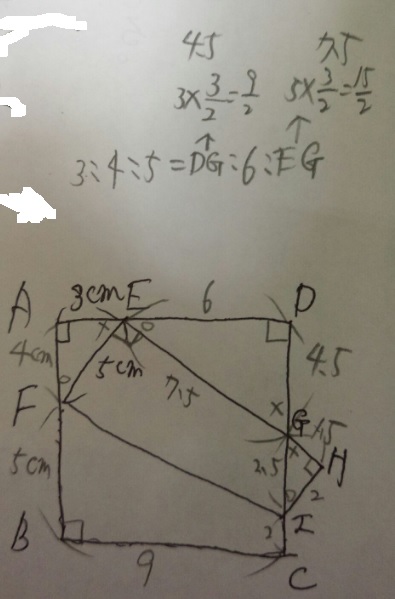
問題)ABCDは1辺9cmの正方形。FIを折り返しています。頂点BがEと
重なりました。(1)EG何cm?(2)GI何cm?
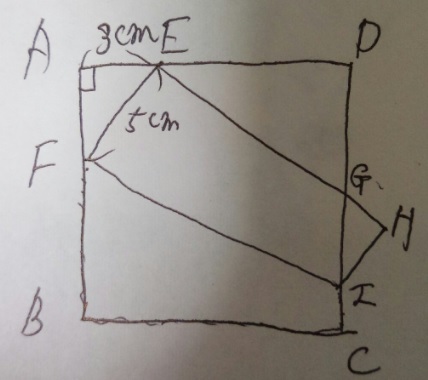
ポイントは折り返してできる三角形はすべて相似!
1)わかる部分を図に書き込みます(頭で解かずに図を書くこと!!!)
2)1)が正確にできれば、後は相似比を元にして計算できます
なお、このパターンでは、中学受験に良くでる【ピタゴラス数】3:4:5がよく出ます。
(関連記事)直角三角形の相似(「3:4:5」「5:12:13」)

▲三角形AEF:DGE:HGIは相似(対応する辺・角度に注意)
▲AF=3:4:5から4(又は9-5)、ED=9-3=6、相似比AEF4(2):DGE6(3)
▲AE3:DG(3×2/3=9/2=4.5)、FE5:EG(5×2/3=15/2=7.5)、EG=7.5cm
▲GH=9-7.5=1.5、GH1.5:GI?の比率は③:⑤、よってGI=1.5×5/3=7.5/3=2.5、GI=2.5cm
答え)(1)7.5cm(2)2.5cm
折り返してできる三角形はすべて相似!の中学入試問題等
問題)明治大学付属中野中学
ABCDは1辺9cmの正方形。FはAF2:FB1、BE4cmの所でCがFに来るように
折り返しました。斜線部分の面積は?
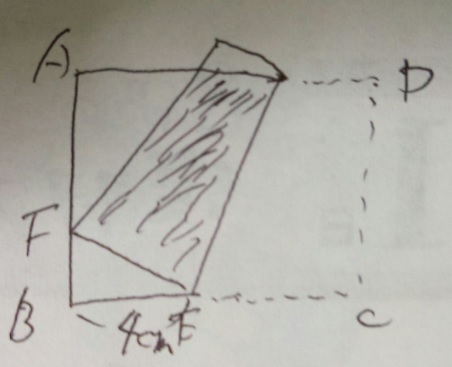
解き方)台形から三角形の面積を引く感じですかね?とりあえず分かる数字を入れます。
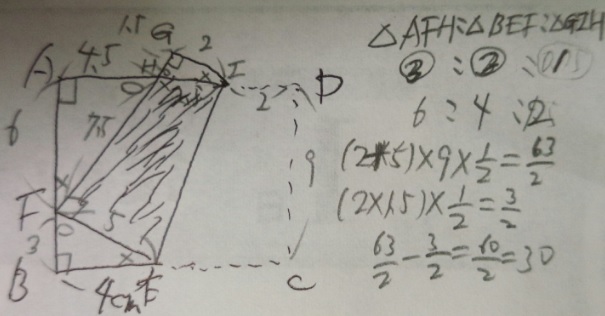
1)FE=5cm(9-4)、3:4:5の直角三角形なのでFB=3,AF=6
2)三つの三角形が相似なのはもういいですね?対応する辺を間違えずに相似比から辺の長さを計算
ポイントは折り返してできる三角形はすべて相似!
3)台形GIFEの面積は(2+5)×9×1/2=63/2c㎡
4)三角形GHIの面積は、1.5×2÷2=1.5(3/2)c㎡
5)斜線部分の面積=台形GIFEー三角形GHIなので、63/2-3/2=60/2=30
答え)30c㎡

まとめ
「折り返しと相似」のポイントは以下です。
1 「合同」と「相似」に注目
2 折り返してできる三角形はすべて相似(対応する角、辺などを書き込むこと)

(関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)