(関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)
【立体図形で相似比a:bなら体積比は(a×a×a):(b×b×b)】
体積比と相似(立体図形)の基本:回転体・すい台
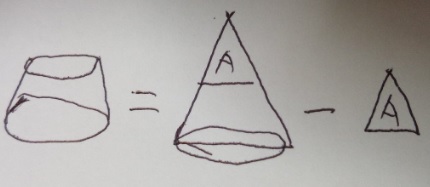
回転体の見取り図の書き方!すい台の体積=すい体ー切られた部分!
「図形+相似」は回転体やすい台のものが多いです。
問題)下記のすい台の体積を求めてください。円周率3.14
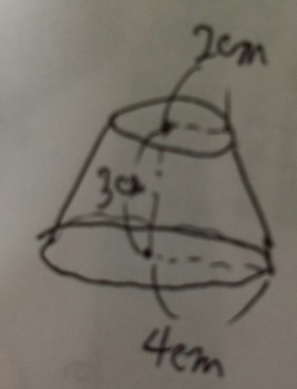
「図形+相似」の典型パターンです。
解法)1)補助線引いてすい体にします
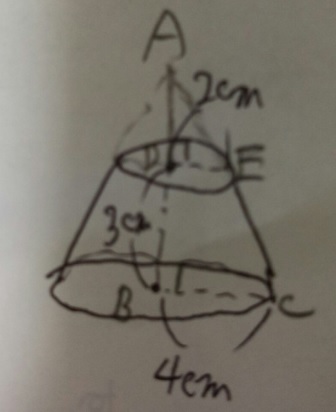
2)相似の三角形を確認
3)でかい円すいー小さい円すい=すい台
・三角形ABCと三角形ADEは相似(2つの角度が同じ)。相似比4:2=2:1
・相似比2:1なのでAD=3cm
・大きい円すいの体積=4×4×3.14×6×1/3=32×3.14=100.48cm3
・小さい円すいの体積=2×2×3.14×3×1/3=4×3.14=12.56cm3
100.48-12.56=87.92cm3
上記の計算はもちろん「分配法則」を使って簡単にするべきです。
4×4×3.14×6×1/3=32×3.14ー2×2×3.14×3×1/3
32×3.14-4×3.14=(32-4)×3.14=28×3.14=87.92
答え)87.92cm3
~~~~~~~~~~~~~~~~~~~~~~~~
すい体の体積=底面積×高さ×1/3(「体積」なので単位はcm3)
すい体の表面積=底面積+側面積
すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
~~~~~~~~~~~~~~~~~~~~~~~
立体図形で相似比a:bなら体積比は(a×a×a):(b×b×b)
そのままです。【立体図形で相似比a:bなら体積比は(a×a×a):(b×b×b)】
例えば先ほどの問題、


三角形ABCと三角形ADEは相似(2つの角度が同じ)。相似比4:2=2:1
円すい大と円すい小の相似比も2:1→体積比(2×2×2):(1×1×1)=8:1
・円すい大の体積=4×4×3.14×6×1/3=32×3.14=100.48cm3
・円すい小の体積=2×2×3.14×3×1/3=4×3.14=12.56cm3
100.48:12.56=8:1 です。
試しに、100.48÷12.56やってみてください。「8」になります。
同じですが、12.56×8=100.48です。
【立体図形で相似比a:bなら体積比は(a×a×a):(b×b×b)】
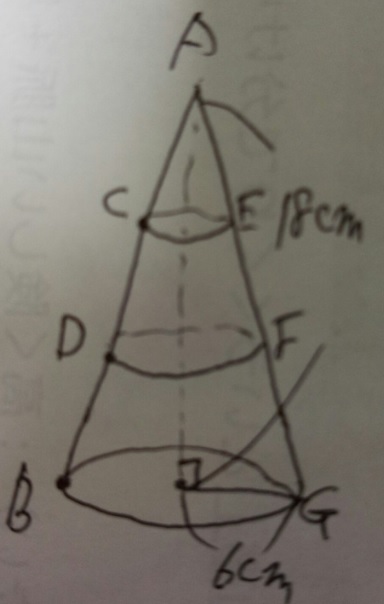
問題)円すいです。C、DはABを三等分した点。3つの円すいはすべて平行。
CEとDFでできるすい台の体積は?円周率は3.14

解法)
1)円すい大・中・小はすべて相似ですね。相似比は、3:2:1ですね?
2)相似比3:2:1なので、体積比は大「27」:「中8」:「小1」
3)求めるのは「円すい中ー円すい小」の体積なので体積比「7」
【立体図形で相似比a:bなら体積比は(a×a×a):(b×b×b)】
4)円すい大の体積=6×6×3.14×18×1/3=678.24cm3
5)678.24が割合「27」で求める割合は「7」なので、
678.24×7/27=25.12×7=175.84
答え)175.84cm3
【立体図形で相似比a:bなら体積比は(a×a×a):(b×b×b)】
体積比と相似:立体図形で相似比a:bなら体積比は(a×a×a):(b×b×b)の中学入試問題等
問題)ラ・サール中学
台形です。中心線を一回転させてできる立体の表面積を求めてください。円周率は3.14
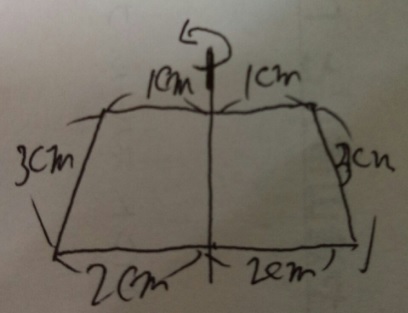
解法)
1)1回転なので円すい台になります。補助線引いて円すいにします
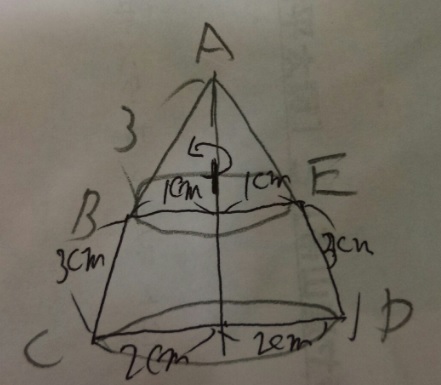
2)求めるのは「円すいACDの側面積-円すいABEの側面積+円すいABEの底面積+円すいACDの底面積」です
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
すい体の体積=底面積×高さ×1/3(「体積」なので単位はcm3)
すい体の表面積=底面積+側面積
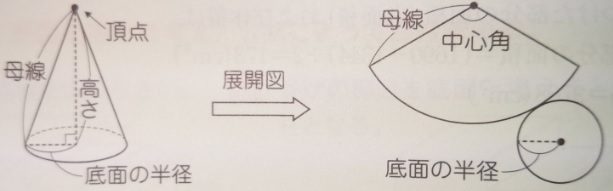
1)(側面の)おうぎ形の中心角=360°×底面の半径/母線
2)円すいの側面積=母線×底面の半径×3.14(円周率)
すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(求めるのは「円すいACDの表面積-円すいABEの側面積+円すいABEの底面積」)
円すいACD:底面積2×2×3.14=12.56、側面積6×2×3.14=37.68
表面積=12.56+37.68=50.24 50.24cm2
円すいABE:底面積1×1×3.14=3.14、側面積3×1×3.14=9.42
表面積=3.14+9.12=12.56cm2
求めるのは「円すいACDの側面積-円すいABEの側面積+円すいABEの底面積+円すいACDの底面積」
「37.68-9.42+3.14+12.56」=43.96
答え)43.96cm2

まとめ
【立体図形で相似比a:bなら体積比は(a×a×a):(b×b×b)】
すい体(三角すい・四角すい・円すい)の公式とテクニック!円すいがポイント!