「影と相似」?知らんがな!だと思いますが、中学受験の算数の入試問題によく出ます・・・。
影と相似のポイント
・太陽は平行に進む!点光源は拡がりながら進む!
・「横から見た図」と「真上から見た図」に【光の線】を書く
・図の中の三角形は(基本的に)相似になる
つまり、「影の問題」は相似・相似比を使って解くという事です。
図を見ないと良く分かりませんね。
影と相似のポイント:太陽は平行に進む!点光源は拡がりながら進む!
イメージすれば分かりますが、太陽光は平行に進みます。電球や街灯などは、
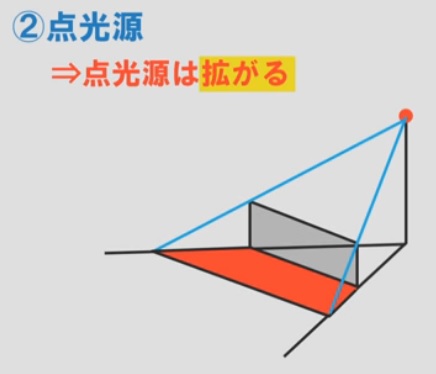
一点から進む「点光源」なので、拡がりながら進みます。
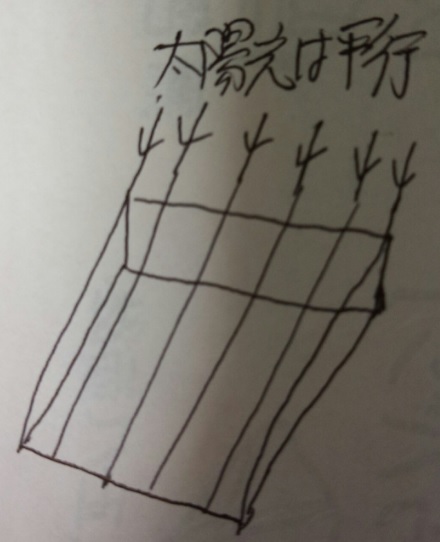
太陽の光は平行なので(同時刻なら)高さが違うと相似の三角形の影になる
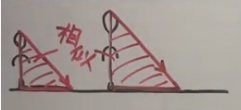
こんなイメージです。高さが違う相似の三角形になります。
(左)Aと影の比が3:2なら、(右)Bとその影の比も3:2となります。
もちろん、建物とその影の比も、人と影の比も、同時刻の同じ場所なら
同じ比率(相似)になります。
問題)だろう君が学校の側で影の長さを計りました。だろう君の身長は150cm、
影の長さは1mでした。校舎の影の長さは12mでした。校舎の高さは?
解法)
1)同時刻+太陽光なので高さと影の長さは比例します(相似)
2)図を書きましょう:正確に書ければほぼ問題は解けています
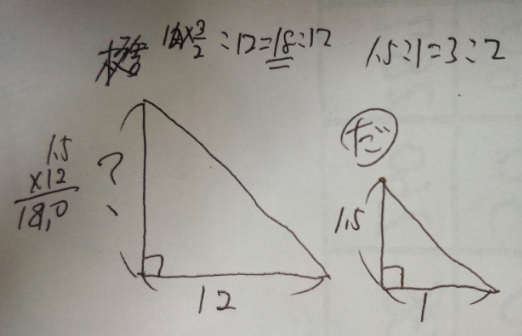
3)相似比にしたがって計算する:縦と横の比は1.5:1=3:2、?:12=3:2、?=12×3/2=18
答え)18m
*古代ギリシャの哲学者タレス(紀元前624~紀元前546頃)は、ピラミッドの高さを
はかるのに影の長さを使ったことで知られています
点光源は「横から見た図」と「真上から見た図」に【光の線】を書く
点光源は拡がりながら進むので、
「横から見た図」と「真上から見た図」に【光の線】を書く
というやり方になります。
出典:https://jukensansuu.com/souji5.html
「真横から見た図 → 真上から見た図」の順に、上下にならべて書くと
かなり解きやすくなります。
出典:https://jukensansuu.com/souji5.html
影と相似の中学入試問題等
問題)城北中学
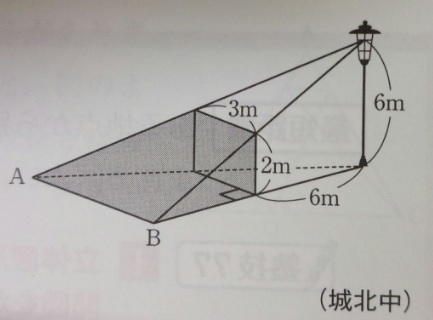
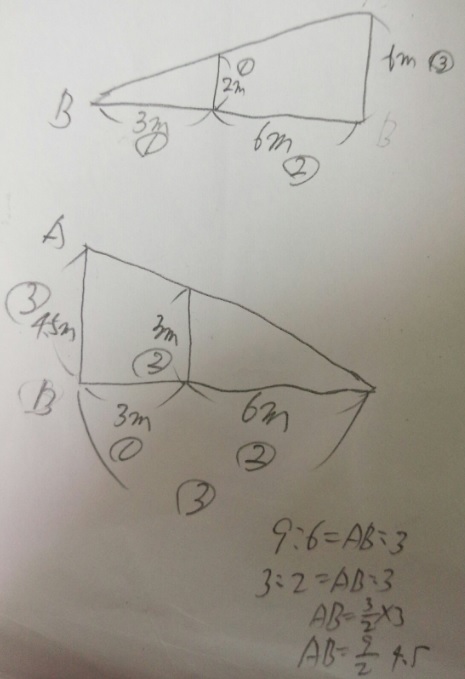
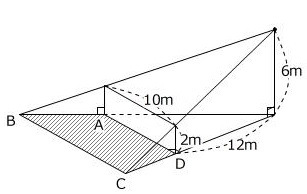
高さ6mの街灯から6m離れた所に高さ2m、幅3mの長方形のへいがあります。
(へいの厚さは考えません)
(1)影の先端の長さ(AB)は?
(2)へいによって陰になっている部分の体積は?
まずは(1)を確実にできるようにしましょう。
解法)
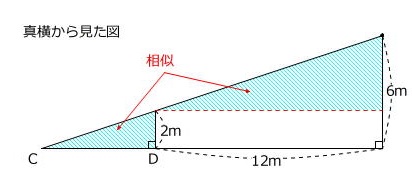
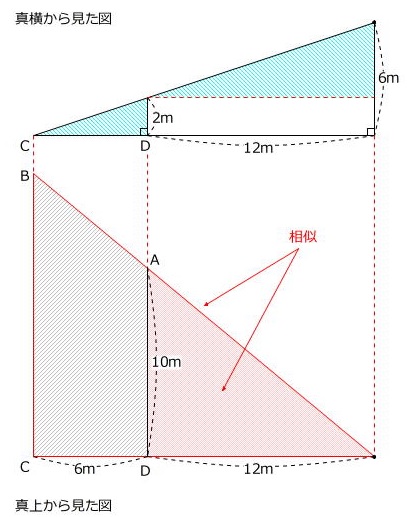
1)「真横から見た図 → 真上から見た図」の順に、上下にならべて書く

2)上が真横から見た図、下が真上から見た図です。相似を使って計算すると
AB=4.5mです。
(2)へいによって陰になっている部分の体積は?
これは簡単ではありませんが、下記を覚えていればできるのでは?(今覚えて)
立体図形を斜めに切断した時の体積は【底面積×高さの平均】
立体図形を斜めに切断した時の体積は【底面積×高さの平均】(この記事に詳細あり)


底面積を真横から見た三角形にすると、3×2×1/2=3
高さの平均は、へいの上下(3と3)とAB4.5なので、
(3+3+4.5)÷3=10.5/3
立体図形を斜めに切断した時の体積は【底面積×高さの平均】
3×10.5/3=10.5 10.5m3
答え)(1)4.5m (2)10.5m3
問題)昭和女子大附属昭和中学
30cmの棒を地面に垂直に立てたら影が40cmできました。同時刻・同じ場所で
図のような木では地面より1m高い土地の4mの所まで影ができました。木の高さは何m?
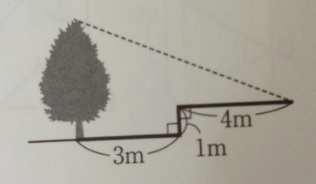
解法)
1)分かっている図を二つ書きます(棒と木)
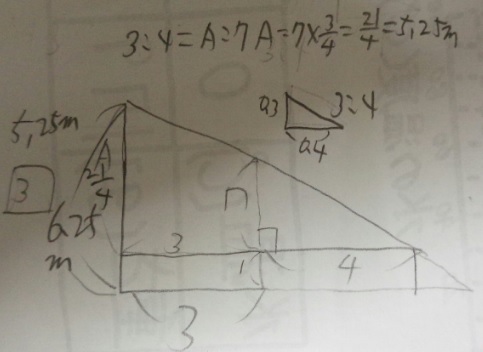
2)棒と影の関係から、三角形の相似比は③:④
3)図のように補助線を引くと、横7mの三角形ができる。これも相似。
4)縦と横の相似比は③:④なので、A:7=③:④→A=7×3/4=21/4=5と1/4=5.25m
5)5.25mの下に1m分あるので、縦(木の長さ)は6.25m
答え)6.25m
まとめ
影と相似のポイント
・太陽は平行に進む!点光源は拡がりながら進む!
・「横から見た図」と「真上から見た図」に【光の線】を書く
・図の中の三角形は(基本的に)相似になる
つまり、「影の問題」は相似・相似比を使って解くという事です。


点光源は拡がりながら進むので、
「横から見た図」と「真上から見た図」に【光の線】を書く
というやり方になります。

出典:https://jukensansuu.com/souji5.html
(関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)
体積比と相似:立体図形で相似比a:bなら体積比は(a×a×a):(b×b×b)
影と相似のポイント:太陽は平行に進む!点光源は拡がりながら進む!+横から見た図と真上から見た図!