図形+【最短距離・反射】の問題は「展開図」を書けるかどうかがポイントです。
最短距離と反射は【展開図】を書いて一直線にする!
最短距離と反射は【展開図】を書くと解ける!
図形の最短距離は【展開図】
問題)EからI経由でCまで糸を張ります。糸が最短距離を通る時BIは何cm?
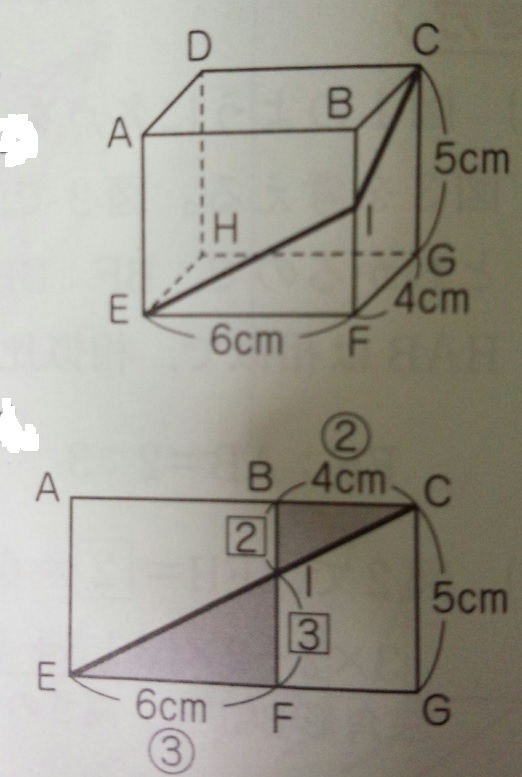
出典:『塾技100算数』p160
最短距離と反射は【展開図】を書いて一直線にする!
解法)
1)(必要な部分の)展開図を書きます(ABEFとBCFGだけでOK)
2)3点を直線で結ぶ(最短距離なので)。これで実質終りです。
3)相似比等で必要な部分の長さを求める
4)三角形EIFとCIBは相似で相似比6:4→③:②
5)BF5cmでそこを割合③と②(BI)に分けているので、BI=2cm
答え)2cm

出典:『塾技100算数』p160
図形と反射も【展開図】
図形と反射も【展開図】が書けるかどうかがポイントです。
反射の場合は、線対称に図形をつなげて反射経路を直線にします。
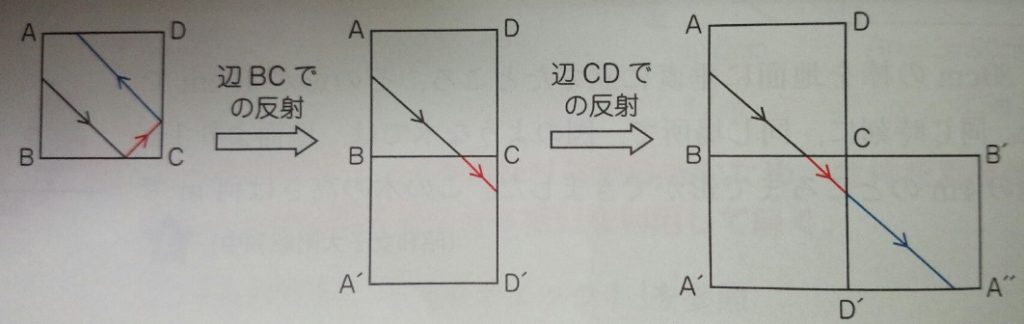
出典:『塾技100算数』p160
こんなイメージです。コツとしては上記であれば、
1)BCで反射したものがCDに向かっているのでそれに合わせて四角を回転させる
2)同じく、CDに反射したものがDAに向かっているのでそれに合わせて回転
3)上記を一直線に結ぶ
となります。
最短距離と反射は【展開図】を書いて一直線にする!
最短距離と反射の中学入試問題等
問題)AQ-QP-PFは最短距離です。PGの長さは?
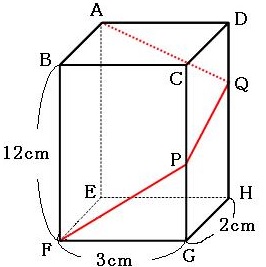
解法)
1)何はなくとも【展開図】(これが書ければ9割は解けています)
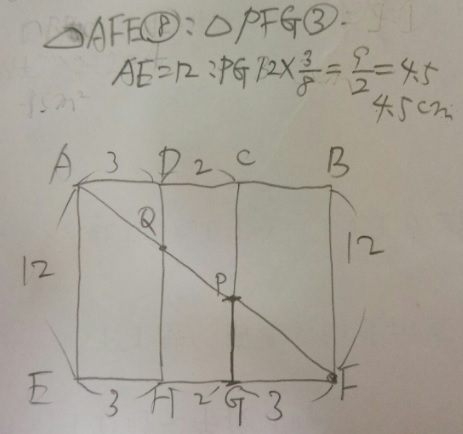
2)あとは相似比の計算のみ。8(3+2+3):3→12:PG, PG=12×3/8=9/2=4.5
答え)4.5cm
問題)独協中学入試問題
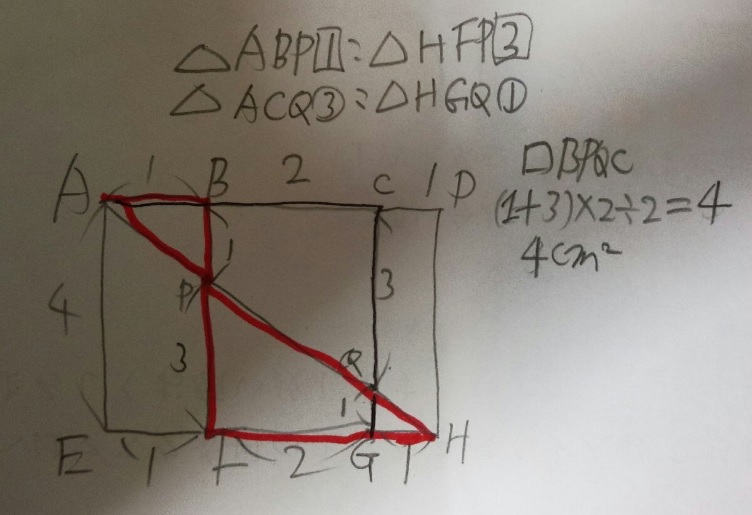
APQHを結ぶ線は最短経路です。四角形BPQCの面積は?
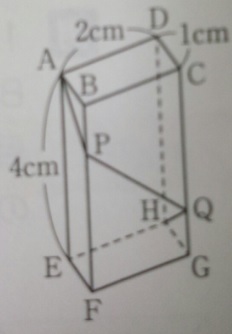
最短距離と反射は【展開図】を書いて一直線にする!
1)展開図を書きAPQHを一直線・最短距離にします(これが正確に書ければ問題の9割は解けています)

2)相似の三角形の組み合わせから、BP1cm、CQ3cmと分かります
3)四角形BPQC=(1+3)×2÷2=4
答え)4cm2
まとめ
図形+【最短距離・反射】の問題は「展開図」を書けるかどうかがポイントです。
最短距離と反射は【展開図】を書いて一直線にする!
(関連記事)
辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える)
体積比と相似:立体図形で相似比a:bなら体積比は(a×a×a):(b×b×b)
影と相似のポイント:太陽は平行に進む!点光源は拡がりながら進む!+横から見た図と真上から見た図!